Moment
Moment[data,r]
gives the order r![]() moment
moment ![]() of data.
of data.
Moment[data,{r1,…,rm}]
gives the order {r1,…,rm} multivariate moment ![]() of data.
of data.
Moment[dist,…]
gives the moment of the distribution dist.
Moment[r]
represents the order r![]() formal moment.
formal moment.
Details


- Moment is also known as a raw moment.
- For scalar order r and data being an array
 :
: -
![x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n] x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n]](Files/Moment.en/7.png)

sum of r 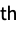 powers »
powers »![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/Moment.en/10.png)

columnwise sum of r 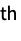 powers »
powers »![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/Moment.en/13.png)

columnwise sum of r 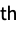 powers »
powers » - Moment[x,r] is equivalent to ArrayReduce[Moment[#,r]&,x,1].
- For vector order {r1,…,rm} and data being array
 :
: -
![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/Moment.en/17.png)

sum the rj 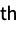 power in the j
power in the j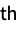 column
column![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/Moment.en/21.png)

sum the rj 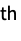 power in the j
power in the j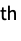 column »
column » - Moment[x,{r1,…,rm}] is equivalent to ArrayReduce[Moment[#,
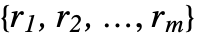 ]&,x,{{1},{2}}].
]&,x,{{1},{2}}]. - Moment handles both numerical and symbolic data.
- The data can have the following additional forms and interpretations:
-
Association the values (the keys are ignored) » WeightedData weighted mean, based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channels values or grayscale intensity value » Audio amplitude values of all channels » - For a distribution dist, the r
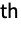 moment is given by Expectation[xr,xdist]. »
moment is given by Expectation[xr,xdist]. » - For a multivariate distribution dist, the {r1,…,rm}
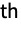 moment is given by Expectation[x1r1⋯ xmrm,{x1,…,xm}dist]. »
moment is given by Expectation[x1r1⋯ xmrm,{x1,…,xm}dist]. » - For a random process proc, the moment function can be computed for slice distribution at time t, SliceDistribution[proc,t], as μr[t]=Moment[SliceDistribution[proc,t],r]. »
- Moment[r] can be used in functions such as MomentConvert, MomentEvaluate, etc. »
Examples
open allclose allBasic Examples (2)
Scope (22)
Basic Uses (6)
Exact input yields exact output:
Approximate input yields approximate output:
Find moments of WeightedData:
Find a moment of EventData:
Find a moment of TimeSeries:
Array Data (5)
For a matrix, Moment gives columnwise moments:
For an array, Moment gives columnwise moments at the first level:
Multivariate Moment for an array:
When the input is an Association, Moment works on its values:
SparseArray data can be used just like dense arrays:
Find the moment of a QuantityArray:
Image and Audio Data (2)
Channelwise moment of an RGB image:
Moment intensity value of a grayscale image:
On audio objects, Moment works channelwise:
Distribution and Process Moments (5)
Scalar moment for univariate distributions:
Scalar moment for multivariate distributions:
Joint moment for multivariate distributions:
Compute a moment for a symbolic order r:
A moment may only evaluate for specific orders:
A moment may only evaluate numerically:
Moments for derived distributions:
Moment function for a random process:
Find a moment of TemporalData at a time t=0.5:
Find the corresponding moment function together with all the simulations:
Formal Moments (4)
TraditionalForm formatting for formal moments:
Convert combinations of formal moments to an expression involving Moment:
Evaluate an expression involving formal moments μ2+μ3 for a distribution:
Find a sample estimator for an expression involving Moment:
Applications (10)
Moments for Data and Time Series (3)
The law of large numbers states that a sample moment approaches a population moment as the sample size increases. Use Histogram to show probability distribution of a second sample moment of uniform random variates for different sample sizes:
Visualize the convergence process:
Compute a moving moment of a time series data:
Compute moments for slices of a collection of paths of a random process:
Method of Moments (3)
Estimate parameters of a distribution using the method of moments:
Compare the data with the estimated parametric distribution:
Find normal approximation to GammaDistribution using the method of moments:
Compare the original and the approximated distributions:
Moments of PearsonDistribution satisfy a three-term recurrence equation implied by the defining differential equation for the density function ![]() :
:
Use the recurrence equation to express parameters of PearsonDistribution in terms of its moments:
Fit PearsonDistribution to data:
Check that moments of the resulting distribution are equal to moments of data:
PDF Approximations from Moments (3)
Two different distributions can have the same sequence of moments:
Compare their densities on log-scale:
Prove them equal for all non-negative integer orders:
Build type A Gram–Charlier expansion of order 6:
A monotone PDF ![]() with a positive domain is bounded by
with a positive domain is bounded by ![]() :
:
Prove the identity for exponential distribution for the first few orders:
Expectation Approximation from Moments (1)
Find quadrature rule for approximating the expectation of a function of a random variable:
Find ![]() lowest-order orthogonal polynomials:
lowest-order orthogonal polynomials:
Find quadrature weights, requiring rule to be exact on polynomials of order up to ![]() :
:
Compute approximation to expectation of ![]() :
:
Check with NExpectation:
Properties & Relations (8)
Moment of order r is equivalent to Expectation of the power r of the random variable:
A multivariate moment is equivalent to Expectation of a multivariate monomial:
For univariate distributions, Moment of order one is the Mean:
Mean of a multivariate distribution is a list of moments of its univariate marginal distributions:
Alternatively, use Moment with orders given by unit vectors:
Moment of order ![]() is the same as
is the same as ![]() when both exist:
when both exist:
Use Moment directly:
Find the moment-generating function by using GeneratingFunction:
Compare with direct evaluation of MomentGeneratingFunction:
Moment can be expressed through CentralMoment, Cumulant or FactorialMoment:
Sample moments are unbiased estimators of population moments:
Hence the sampling distribution expectation of the estimator equals the estimated moment:
Verify this on a sample of fixed size; evaluate the estimator on the sample:
Find its expectation assuming independent identically distributed random variables ![]() and
and ![]() :
:
Possible Issues (2)
Neat Examples (2)
Find an unbiased estimator for a product of moments:
Check unbiasedness for a special case of ![]() on a GammaDistribution:
on a GammaDistribution:
The distribution of Moment estimates for 20, 100 and 300 samples:
Text
Wolfram Research (2010), Moment, Wolfram Language function, https://reference.wolfram.com/language/ref/Moment.html (updated 2024).
CMS
Wolfram Language. 2010. "Moment." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Moment.html.
APA
Wolfram Language. (2010). Moment. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Moment.html