Body size prediction in scorpions: a phylogenetic comparative examination of linear measurements of individual body parts

Introduction

Comparative analysis focusing on body size variation has gained popularity in ecological and evolutionary studies. This rise in scientific interest can be attributed to the significant role of body size in influencing and being influenced by various other life-history traits in animals (Peters, 1986; Klingenberg & Spence, 1997; Blanckenhorn, 2000; Kozłowski, Konarzewski & Czarnoleski, 2020; Johnson et al., 2023). Examples of these well-known associations include relationships linking body size with range size (Noonan et al., 2020; Seifert, Strutzenberger & Fiedler, 2022), dispersal capability (Alzate & Onstein, 2022), mobility (Kuussaari et al., 2014), thermal regulation (Gardner et al., 2011), fecundity (Tammaru, Esperk & Castellanos, 2002), longevity (Holm et al., 2022; Kuparinen, Yeung & Hutchings, 2023), dietary specialization (Seifert, Strutzenberger & Fiedler, 2023), and sexual selection (Janicke & Fromonteil, 2021), among others.

Body size is typically represented by weight (mass) or length, depending on how conveniently and accurately these measures can be obtained for the taxonomic group under study. For invertebrates, particularly arthropods, measures of weight can serve as a good proxy for body size when aiming to capture both size and shape within a single value (e.g., Kendall et al., 2019; Ruiz-Lupión, Gómez & Moya-Laraño, 2020; Foerster et al., 2024a, 2024b; Ude et al., 2024), or in the analysis of metabolic rates and energy allocation (e.g., Llandres et al., 2015; Ferral et al., 2020; Turnbull, McNeil & Sinclair, 2023). However, using weight measurements often requires handling hundreds of individuals under laboratory conditions. For instance, if dry mass is employed, animals must be sacrificed and transferred to a laboratory for proper processing, often involving specialized equipment. Moreover, body weight rather than body length is expected to be more influenced by factors such as water and fat content, nutritional condition, and reproductive stage (Chown & Gaston, 2010; Stahlschmidt & Chang, 2021). These factors can produce transient changes in body weight that may not accurately reflect the actual body size of the organism. Length measures, in contrast, provide a simpler solution to overcome such challenges. In most cases, length measures can be directly obtained in the field without the need for specialized equipment. In addition, for non-flying arthropods, length measures of body size are typically expressed as the total length of the animal without appendages, which can be thus considered a homologous trait across the studied species (Ruiz-Lupión, Gómez & Moya-Laraño, 2020).

Using length measures offers another advantage: specific body parts can be used to represent body size itself. This is made possible by allometry, where body parts scale in size relative to overall body size (Pélabon et al., 2018). By studying the allometric properties of a readily measurable trait, one can use its measurements to estimate body size or directly represent body size itself. This approach proves useful when directly measuring body size (e.g., total length) is more labor-intensive, being commonplace in ecological and evolutionary studies with several invertebrate groups (e.g., Warzecha et al., 2016; Austin et al., 2022; Jahant-Miller, Miller & Parry, 2022; Lira et al., 2021; Lira, Andrade & Foerster, 2023; Staton et al., 2023). Not surprisingly, significant efforts have been directed towards developing predictive models (equations) of body size based on meristic traits that are simpler to measure (Kendall et al., 2019; Foerster et al., 2024a). This includes “classical” linear predictive equations on a log-log scale (Huxley, 1932; Packard, 2013; Pélabon et al., 2018), which are commonly employed to predict body size in various insect groups, including (but not limited to) Coleoptera, Isoptera, Thysanura (Ruiz-Lupión, Gómez & Moya-Laraño, 2020), Hymenoptera (Kendall et al., 2019; Ruiz-Lupión, Gómez & Moya-Laraño, 2020), Lepidoptera (Foerster et al., 2024a), Diptera (Kendall et al., 2019) and, to a lesser extent, in other arthropods, such as arachnids (Hódar, 1996, 1997; Höfer & Ott, 2009; Shiao et al., 2019).

Simpler proxies and predictive models for estimating body size are especially valuable for arachnids, especially those belonging to clades with complex body architecture. Directly measuring the total length of scorpions, for instance, can be methodologically challenging due to their overall body structure. The nearly 2,830 extant scorpion species described to date (Rein, 2024) share a characteristic body structure consisting of three main segments: the prosoma, mesosoma, and metasoma. Obtaining precise measurements of total length in scorpions requires stretching anatomical parts such as the metasoma, commonly referred to as “tail”, which demands considerable time and expertise. Procedures like these are impractical to be performed on live specimens, being also problematic for museum specimens without the considerable risk of causing damage to the individual, which in turn, affects the precision of the measurements. This is likely one of the reasons why carapace length is frequently used as a proxy for body size in scorpions (e.g., DeSouza et al., 2016; Seiter & Stockmann, 2017; Lira, Andrade & Foerster, 2023; Moreira et al., 2022; Giménez Carbonari et al., 2024), despite the lack of empirical evidence demonstrating its suitability as an indicator of body size, at least in comparative contexts. However, even carapace length cannot always be easily measured. In some instances, the carapace itself can be damaged, or its edges may be covered by other body parts, such as the pedipalps, necessitating handling that also increases the risk of structural damage to the specimen. Therefore, models that enable accurate prediction of body size measurements in scorpions (e.g., total length, carapace length) from simpler linear measurements of various body parts are valuable tools, particularly when dealing with highly damaged or fragile specimens. In some cases, these models represent the only alternative to obtaining information on body size, such as with old and poorly preserved specimens from scientific collections and some fossil records.

The aim of this study is to establish coefficients for accurately predicting body size in scorpions, while considering their evolutionary history. I present a series of simple linear equations implemented in custom R functions that can be used to effectively predict total length and carapace length—two commonly used measures of body size in scorpions (e.g., Outeda-Jorge, Mello & Pinto-da-Rocha, 2009; Seiter & Stockmann, 2017; Lira et al., 2018; Lira, Andrade & Foerster, 2023; Giménez Carbonari et al., 2024) based on simple linear measurements of individual body parts. Specifically, I assessed the predictive power of seven linear measurements using simple and multiple phylogenetic mixed linear models across 195 scorpion species from the family Buthidae. The family Buthidae is the most species-rich clade within the order Scorpiones, offering sufficient morphometric variation to effectively represent the order in terms of overall body size as well as the size and shape of individual body parts.

Materials and Methods

Trait data and species

Linear measurements were primarily obtained from a comprehensive list of taxonomic and ecological studies on buthid scorpions (Supplemental file S1). The measurements were mainly presented in simple tables that could be manually retrieved from the selected articles. The present study acknowledges that while measurement errors in the selected traits can be minimized, they cannot be entirely eliminated. However, it is assumed that these errors do not significantly impact the quality of size predictions, as (1) the articles selected for extracting the meristic information were mostly authored by experienced scorpion taxonomists, and (2) the models are intended to provide an average estimate of body size rather than precise, exact predictions.

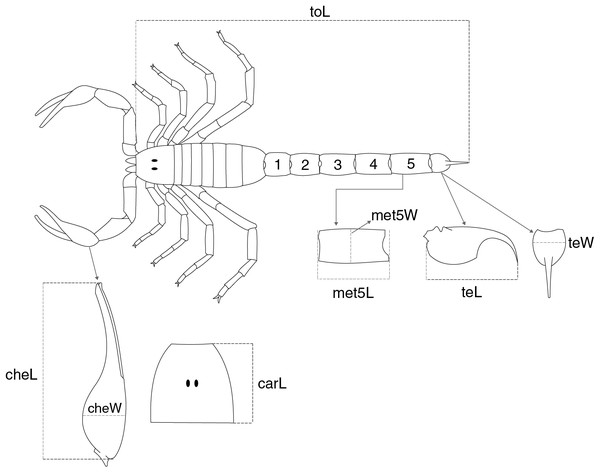
Two proxies for body size were employed in this study (analyzed separately, see below): total length (toL), measured from the anterior margin of the carapace to the aculeus tip (Fig. 1), and carapace length (carL), expressed by the maximum distance between the anterior and the posterior margins of the carapace (Fig. 1). The candidate traits used as predictors of the two body size measures are illustrated in Fig. 1. These included: chela length (cheL) measured from the base of the manus to the tip of the fixed finger, chela width (cheW) measured dorsally at the middle of the manus, telson length (teL) obtained from the distance connecting the base of the vesicle to the aculeus tip, telson width (teW) corresponding to the width of the vesicle in dorsal view, and the length (met5L) and width (met5W) of the metasomal segment V (Fig. 1; Sissom, Polis & Watt, 1990); the ability of carL in predicting toL was also evaluated. The (predictor) measurements were chosen because they are relatively easy to measure in well-preserved specimens and readily available in taxonomic studies of scorpions (Supplemental file S1).

Raw trait values were used to calculate species means separately for males and females for species represented by more than one individual per sex. On average, two individuals per sex were used to calculate species means for each species (Supplemental file S1). The proportion of missing data in the trait matrices ranged from 2% (cheL in both sexes) to 13% (teW in males). Missing predictor trait values in both matrices were imputed using the missForest R package (Stekhoven & Bühlmann, 2012) due to its accuracy and computational efficiency (Penone et al., 2014; May, Feng & Adamowicz, 2023). Imputation was performed separately for each sex using the log-transformed species means. Phylogeny was incorporated by including the first 10 eigenvectors from a principal coordinate analysis on cophenetic distances (Penone et al., 2014) calculated from an ultrametric phylogeny generated in this study (see below) in each trait matrix.

A second analysis was performed to assess the precision of the imputation procedure on each trait matrix (one per sex). It consisted in pruning the trait matrices to retain only species with no missing data (n = 119) in the original scale (mm). Then, 13% of data—the maximum proportion of missing data observed in the original matrices—was randomly assigned as missing data in each trait in the pruned matrices. The imputation was performed on the pruned matrices with their respective phylogenetic eigenvectors, and the imputation accuracy was assessed using the normalized root mean square error (NRMSE), which compares predicted and actual values, with values closer to zero indicating higher accuracy (Stekhoven & Bühlmann, 2012). The imputation on the pruned matrices was repeated 10 times for each sex, and the mean NRMSE (in mm) was reported for each.

Results

General findings

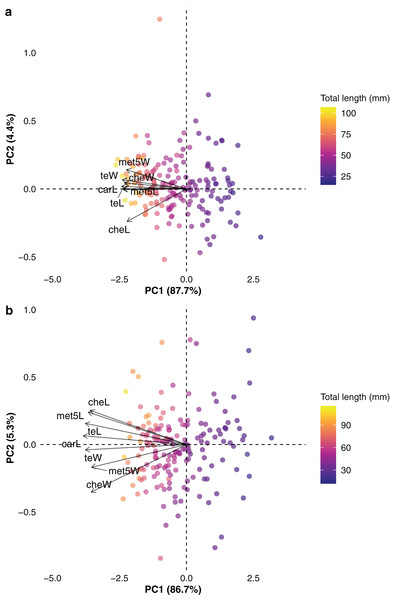
Total length ranged from 14.9 to 116.2 mm in females (mean ± standard deviation: 53.7 ± 20.8 mm) and 11.9 to 119.1 mm in males (50.6 ± 20.6 mm). Measurements of carapace length ranged from 2 to 12.5 mm in females (5.9 ± 2.2 mm) and 1.6 to 10.9 mm in males (5.3 ± 2.1 mm). The phylogenetic trait imputation performed on the missing values for predictor traits proved to be highly accurate, with mean NRMSE (calculated across 10 iterations) of 0.01 mm for both sexes. The visual inspection of the trait space through phylogenetic PCA indicated high correlation between the studied traits (Figs. 2A, 2B), which was corroborated by the high trait loadings on the phylogenetic PC1 (Table 1). Specifically, all traits correlated more strongly (and in the same direction) with PC1, indicating that PC1 effectively captured size (length) information. The strength and direction of trait correlations in relation to PC1 indicated a size gradient along this axis. Smaller species were primarily located on the right side of the size gradient (positively correlated with PC1), while larger species occupied the left side of the gradient (negatively correlated with PC1). Species appeared more dispersed in the two-dimensional trait space of male data (Fig. 2B) compared to the trait space constructed from female data. Additionally, smaller species tended to be more widely distributed in the bidimensional trait space for both sexes, though this pattern was more pronounced in males (Fig. 2B). The tree topology and node age estimations were largely consistent with previous phylogenetic hypotheses (e.g., Ojanguren-Affilastro et al., 2017; Santibáñez-López et al., 2022; Štundlová et al., 2022), recovering major buthid clades, such as the Tityus and Buthus groups, with strong statistical support (Supplemental file S1). The monophyly of species-rich genera such as Tityus and Centruroides was also well supported (Supplemental file S1). Divergence times were estimated at 57.7 Mya (95% HPD: 53–63 Mya) for the Tityus group and 43.2 Mya (39.7–46.6 Mya) for the Buthus group.

Table 1:

Trait loadings on the first two axes of the phylogenetic principal component analysis performed on linear measurements of body parts of buthid scorpions (n = 195).

	Female		Male
Trait	PC1	PC2	PC1	PC2
Carapace length	−0.97	0.03	−0.98	0.07
Chela length	−0.89	−0.43	−0.91	0.26
Chela width	−0.93	0.08	−0.90	−0.36
Length of metasomal segment V	−0.95	−0.01	−0.93	0.25
Width of metasomal segment V	−0.90	0.25	−0.90	−0.17
Telson length	−0.96	0.0004	−0.96	0.16
Telson width	−0.96	0.12	−0.96	−0.04
Variance (%)	87.70	4.40	86.70	5.30

DOI: 10.7717/peerj.18621/table-1

Note:

Phylogenetic dependence in trait values was accounted for by using the lambda method. All trait values were log-transformed before the analysis.

Predicting total length

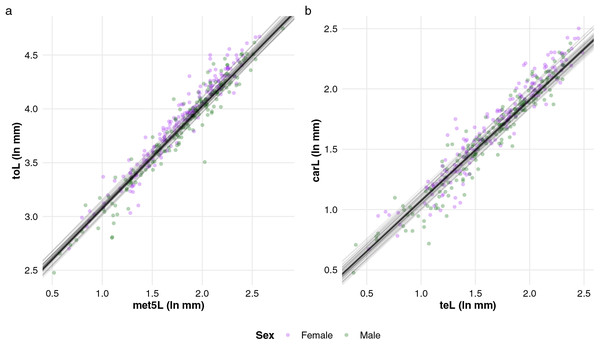
Overall, all studied traits predicted toL with satisfactory accuracy, with RMSE values not exceeding 12.2 mm (Table 2). The most effective single predictor of toL was met5L (RMSE = 6.4), closely followed by carL (Table 2). The linear relationship between met5L and toL was consistent across males and females (Fig. 3A), further supported by the non-significant interaction between met5L and sex, as observed for all other traits used to predict toL (Supplemental file S1). Conversely, met5W proved to be the least accurate single predictor (Table 2), aligning with its lower loadings on the first axis of the phylogenetic PCA, evidencing its limited ability to represent overall size (length) compared to the other traits (Table 1). The coefficients obtained from the model including met5L proved to be efficient in predicting toL in non-buthid scorpions, with differences between predicted and actual values not exceeding 7.5 mm (Table 3).

Table 2:

The performance of linear measurements in predicting (ToL) total length and (CarL) carapace length in buthid scorpions (n = 195) was assessed using Bayesian phylogenetic mixed linear models.

Response	Predictor	RMSE	Coefficients	Mean	Lower	Upper	ESS
toL	met5L	6.41	Intercept	2.13	2.03	2.22	900
			Slope	0.95	0.91	0.99	795
	carL	6.46	Intercept	2.18	2.08	2.27	900
			Slope	1.01	0.97	1.05	900
	teL	7.22	Intercept	2.32	2.21	2.44	1,088
			Slope	0.90	0.86	0.94	900
	cheL	8.84	Intercept	2.27	2.08	2.50	900
			Slope	0.72	0.67	0.78	900
	teW	9.27	Intercept	3.29	3.13	3.44	994
			Slope	0.82	0.77	0.86	900
	cheW	10.70	Intercept	3.40	3.23	3.57	900
			Slope	0.63	0.57	0.69	900
	Met5W	12.24	Intercept	3.13	2.94	3.34	678
			Slope	0.71	0.65	0.77	805
carL	teL	0.68	Intercept	0.24	0.13	0.34	800
			Slope	0.84	0.80	0.87	752
	teW	0.76	Intercept	1.12	0.99	1.22	810
			Slope	0.78	0.74	0.81	1,090
	Met5L	0.96	Intercept	0.10	−0.02	0.22	900
			Slope	0.85	0.80	0.90	900
	cheL	0.98	Intercept	0.22	0.04	0.42	900
			Slope	0.66	0.61	0.71	900
	Met5W	1.02	Intercept	0.95	0.75	1.09	870
			Slope	0.71	0.66	0.76	900
	cheW	1.06	Intercept	1.22	1.08	1.39	1,156
			Slope	0.60	0.55	0.65	900

DOI: 10.7717/peerj.18621/table-2

Note:

See Fig. 1 for trait abbreviations.

All variables were log-transformed (using natural logarithms) before the analysis. Repeated measurements for species (i.e., one measurement per sex) were included as random intercept factors in the models. The equation for predicting the desired body size metric (in mm) is given by: Y = exp(a + ln(x)b), where a is the intercept, x is the predictor, and b is the slope of the predictor. RMSE represents the residual mean squared error, lower and upper 95% credible intervals are presented. ESS, effective sample size.

Table 3:

Size predictions for non-buthid scorpions (n = 30) according to the best-fit phylogenetic simple regression models fitted under a Bayesian framework.

Species	Family	Sex	ToL	ToL Dev.	CarL	CarL Dev.	Source
Vaejovis vorhiesi	Vaejovidae	Female	28.25	−0.36	3.45	−0.09	Ayrey & Soleglad (2015)
Orobothriurus grismadoi	Bothriuridae	Male	30.36	−0.61	3.47	0.85	Ojanguren Affilastro et al. (2009)
Scorpiops kovariki	Scorpiopidae	Female	32.95	−0.68	4.84	−0.39	Tang et al. (2024)
Chaerilus seiteri	Chaerilidae	Male	24.20	−0.80	3.60	0.19	Kovařík (2012b)
Teuthraustes braziliensis	Chactidae	Male	52.20	−1.24	7.50	−0.49	Lourenço & Duhem (2010)
Calchas kosswigi	Iuridae	Female	34.25	−1.53	4.30	0.33	Yağmur et al. (2013)
Typhlochactas mitchelli	Typhlochactidae	Male	8.99	1.68	1.17	0.66	Sissom (1988)
Diplocentrus izabal	Diplocentridae	Male	53.85	1.79	6.75	−0.71	Armas & Trujillo (2016)
Scorpiops tongtongi	Scorpiopidae	Female	41.90	1.82	6.70	−0.85	Tang (2022a)
Megacormus franckei	Euscorpiidae	Female	42.48	−2.12	6.38	−0.53	Kovařík (2019)
Euscorpius gulhanim	Euscorpiidae	Male	26.96	−2.13	3.97	−0.03	Yağmur (2024)
Diplocentrus franckei	Diplocentridae	Male	57.80	2.50	7.10	−2.06	Santibáñez-López (2014)
Balsateres cisnerosi	Vaejovidae	Male	47.00	2.52	6.10	−0.10	González-Santillán & Prendini (2018)
Vaejovis troupi	Vaejovidae	Female	25.70	2.94	3.40	0.04	Ayrey & Soleglad (2015)
Hadrurus anzaborrego	Hadruridae	Male	84.90	−3.32	11.45	−1.38	Soleglad, Fet & Lowe (2011)
Calchas anlasi	Iuridae	Male	28.55	3.43	3.70	0.60	Yağmur et al. (2013)
Chactas moreti	Chactidae	Male	43.10	3.52	5.60	0.40	Lourenço (2014)
Scorpiops deshpandei	Scorpiopidae	Male	54.24	−3.71	8.43	−1.46	Tang et al. (2024)
Urophonius trewanke	Bothriuridae	Male	32.53	3.73	3.71	1.44	Ojanguren-Affilastro et al. (2024)
Euscorpiops thaomischi	Scorpiopidae	Male	45.00	3.79	7.80	−0.86	Kovařík (2012a)
Alpiscorpius lambda	Euscorpiidae	Male	21.13	3.81	3.52	0.09	Kovařík et al. (2019)
Spinochactas mitaraka	Chactidae	Female	12.92	4.33	2.00	0.54	Lourenço (2016)
Qianxie solegladi	Pseudochactidae	Female	24.70	5.05	3.10	0.69	Tang (2022b)
Brachistosternus mattonii	Bothriuridae	Male	54.46	−5.23	5.74	0.66	Ojanguren-Affilastro (2005)
Hadruroides tishqu	Caraboctonidae	Female	57.90	5.26	7.60	0.39	Ochoa & Prendini (2010)
Bothriurus delmari	Bothriuridae	Female	25.90	5.34	3.70	0.43	Santos-Da-Silva, Carvalho & Brescovit (2017)
Hadrurus anzaborrego	Hadruridae	Female	104.30	−5.57	13.20	−1.66	Soleglad, Fet & Lowe (2011)
Chaerilus solegladi	Chaerilidae	Male	45.00	5.96	6.40	0.23	Kovařík (2012b)
Diplocentrus izabal	Diplocentridae	Female	52.25	−6.72	7.50	−1.69	Armas & Trujillo (2016)
Troglotayosicus akaido	Troglotayosicidae	Male	19.53	7.47	3.32	0.33	Moreno-González, Luna-Sarmiento & Prendini (2024)

DOI: 10.7717/peerj.18621/table-3

Note:

Deviances were calculated as the difference between predicted and actual values of toL and carL. All measurements are reported in millimeters.

The multiple regression analyses revealed that total length predictions could be slightly improved by adding a secondary predictor alongside met5L (Supplemental file S1). However, these improvements were modest: the difference in RMSE between the best-fit multiple regression model (met5L + cheW, RMSE = 5.13 mm) and the best single-predictor model was only 1.28 mm.

Discussion

This study explored the ability of linear measurements of specific body parts in predicting the overall body size in buthid scorpions taking phylogenetic relationships among species into account. As a result, several predictive equations that accurately and easily estimate body size metrics such as toL and carL, which are commonly used to express body size in scorpions (e.g., Fox, Cooper & Hayes, 2015; McLean, Garwood & Brassey, 2018), are reported and implemented in custom R functions.

The general lack of statistically significant interactions involving sex indicated that the predictive models can be generalized for size prediction in both male and female scorpions. This is particularly useful in cases where species exhibit subtle morphological differences between the sexes or when specimens are heavily damaged or fragmented in a way that the determination of sex is impossible. The latter scenario may be common in various fields, including paleontology where only partial remains may be available or visible for performing precise measurements (e.g., Santiago-Blay et al., 2004; Riquelme et al., 2015; Lourenço, 2023), and studies of feeding ecology, where only parts of the specimens may be recovered (e.g., Sahley et al., 2015; Nordberg et al., 2018; Karawita et al., 2020; Qashqaei, Ghaedi & Coogan, 2023). Moreover, the predictive equations presented here can also be valuable for obtaining precise measurements of body size for scorpions stored in scientific collections, as the conventional measurement can be challenging without risking damage to the specimen.

The simple phylogenetic regression models indicated that carL was an effective predictor and good proxy for body size (toL), albeit not the best. Although this finding may not sound surprising given that several studies have used carL as an indicator of body size in scorpions (e.g., DeSouza et al., 2016; Seiter & Stockmann, 2017; Moreira et al., 2022; Lira, Andrade & Foerster, 2023; Giménez Carbonari et al., 2024), it constitutes the first empirical validation of the suitability of carL in predicting total length and also as being a reliable proxy for body size in these animals, tested with robust comparative data. With a few exceptions (McLean, Garwood & Brassey, 2018) the use of carL as an indicator of body size is not always clearly justified. From a technical perspective, using carL offers some useful methodological advantages over toL, the most straightforward of them being the ease of measure. Ideally, however, such methodological advantages should be supported by empirical validations obtained from compelling evidence, which the present study now provides.

The visual inspection of trait space provided by the phylogenetic principal component analysis indicated no major differences in the covariation structure of the trait data between sexes, aligning with the general absence of sex-specific slopes in the linear relationships between each trait and the two body size metrics. However, the phylogenetic PCA revealed that species were more widely dispersed in the two-dimensional trait space constructed from male data, particularly for smaller species. This suggests that morphological diversity, in a multivariate context, may be greater in males, supporting previous hypotheses that link sexual selection as a key driver of sexual size dimorphism in scorpions, particularly influencing the size and shape of male body parts (Lira et al., 2018; McLean, Garwood & Brassey, 2018; Visser & Geerts, 2021, but see Sánchez-Quirós, Arévalo & Barrantes, 2012). Besides sexual selection, other selective forces such as predation pressure and resource exploitation are also correlated with body size, in which smaller species are generally more vulnerable to negative impacts, including higher predation rates (Moreira et al., 2022) and foraging constraints (Polis & McCormick, 1987). These adverse effects are likely to be more pronounced in male scorpions, as they tend to be more active on the surface while foraging and seeking mates (Polis, 1990). Therefore, it is plausible that the greater overall dispersion observed in male trait space, especially among the smallest species, reflects, to some extent, these selective forces influencing species morphology.

The size gradient observed along the phylogenetic PC1, supported by the observed trait loadings, suggests that not only do length-related traits contain significant information about overall size, but also traits related to the widths of the chela and telson. These findings indicate that while obtaining a reasonable indicator of size (length) in scorpions is relatively easy, the same cannot be said for reliably capturing information on overall shape. In such a context, morphometric ratios between different body parts or size-normalized trait measurements might offer alternative means of capturing shape-related information. Some morphometric ratios have been utilized as diagnostic characters in a taxonomic context (e.g., Soleglad & Fet, 2010; Kovařík & Lowe, 2022, but see González-Santillán & Prendini, 2015) or in intraspecific analyses of morphological variation (Alqahtani et al., 2022). However, for the purposes of this study, the choice was made to prioritize the primary goal of proposing simple predictive equations capable of accurately estimating body size without the necessity of measuring multiple body parts or calculating secondary variables (i.e., morphometric ratios) for size prediction. Still, the arrangement of trait values within the two-dimensional space of the phylogenetic PCA, together with the magnitude and direction of trait loadings on axis 1, suggests that allometry likely plays a crucial role in determining the size of the traits examined in this study. However, the phylogenetic PCA is unable to clearly reveal the specific allometric patterns associated with each trait—for instance, whether they follow isometry, positive, or negative allometric patterns. Therefore, the findings reported here serve as a foundation for further investigations in this area, which could offer valuable insights not only into the evolutionary forces (such as sexual and natural selection) shaping the morphology of scorpions but also into the evolution of sexual size dimorphism and sexual body component dimorphism (Fox, Cooper & Hayes, 2015) in these animals.

Regarding the predictive ability of the studied traits, the simple phylogenetic regression models indicated that met5L was the best single predictor of toL. Met5L is particularly advantageous for measurement because assessing it typically does not require fully extending the metasoma or manipulating other body parts for obtaining the measurements. Furthermore, metasomal segments are highly sclerotized structures in scorpions, which makes them less prone to breakage compared to other anatomical parts such as the aculeus (part of the telson)—it is not uncommon to encounter individuals with broken aculeus tip (e.g., Armas, 1999; Teruel & Rein, 2010; Teruel & Kovařík, 2014). This issue might be more concerning for the utilization of teL as a predictor of body size, particularly in smaller species because the accuracy of predicting carapace or total length may be compromised in specimens with broken aculeus. The degree of this artifact will vary depending on the amount of aculeus missing relative to the approximate length of the telson. For example, if one considers a hypothetical scenario where an aculeus breakage results in the loss of 1 mm length in the telson of an adult specimen of Centruroides exilimanus Teruel & Stockwell, 2002, it will represent, on average, only 9% of the telson length in this species (average telson length = 10.8 mm, Teruel & Stockwell, 2002; Viquez & Armas, 2005). In contrast, the same damage would correspond (on average) to 68% of the telson length in a specimen of Microtityus fundorai Armas, 1974 (telson length = 1.46 mm, Armas, 1974). Fortunately, all other predictors performed relatively well in estimating both toL and carL. Hence, the general recommendation is to use teL as a predictor of body size only when the telson is fully intact. This is particularly relevant for predicting carL, where teL proved to be the most accurate predictor. In such cases, it might be more advantageous to use teW, as the vesicle (the anatomical region from which telson width is measured) appears to be less prone to damage compared to the aculeus.

Interestingly, the phylogenetic multiple regression models indicated that the inclusion of a secondary predictor did not result in substantial enhancement of body size estimation. This is likely because all predictor traits had a strong size (length) component that was not removed prior to fitting the models. Including a secondary predictor would be more beneficial for body size prediction if that trait provided information on shape rather than just length, as body size is a composite metric incorporating length, width, and height (Sohlström et al., 2018; Foerster et al., 2024a). It is important to note that removing the size component from the predictor traits would not be appropriate in this study, as the methods provided here are designed to estimate body size based on linear measurements of body parts, under the assumption that body size is not known beforehand. Conveniently, comparing the average accuracy of simple and multiple phylogenetic regression models showed that a single predictor is typically sufficient for accurate estimations of toL and carL. This opens the possibility of performing size predictions in scorpions with minimal effort, an assumption that, to some extent, can be generalized to scorpions in general as the best-fit simple regression models resulted in accurate size estimations in non-buthid species. This is particularly suited for working with severely damaged specimens or when the identification at the family level is not possible. Yet, this finding supports the idea that the trait predictors of body size within the Buthidae clade reflect those found in the order Scorpiones. Ultimately, the flexibility of having multiple traits capable of accurately predicting body size through the simple linear equations presented in this study offers researchers a range of options for choosing the most suitable predictor traits.

Conclusions

The predictive equations introduced in this study offer several alternatives for researchers across various fields to precisely estimate body size in scorpions, whether it pertains to total length or carapace length—the primary indicators of body size in these animals. By utilizing the methods outlined here, researchers can generate accurate estimations of body size even in scenarios where the specimens are extensively damaged or only parts of the specimens are available. Furthermore, while the focus of this study has been directed to buthid scorpions, it has been demonstrated that the proposed predictive equations could be applicable to make educated body size predictions in non-buthid scorpions, particularly those sharing similar morphological characteristics in the examined traits and within the same size range as buthid scorpions. These may also include fossil records, though it is important to consider that size predictions for older and phylogenetically distant fossils may not be as accurate as those made for extant buthid species—an issue that is not exclusive to the present research.

Supplemental Information