Tarjan's Algorithm to find Strongly Connected Components
Last Updated :
06 Jun, 2023
A directed graph is strongly connected if there is a path between all pairs of vertices. A strongly connected component (SCC) of a directed graph is a maximal strongly connected subgraph. For example, there are 3 SCCs in the following graph:
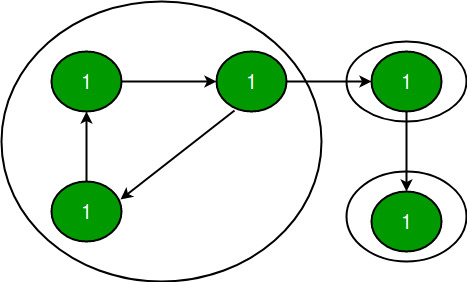
We have discussed Kosaraju's algorithm for strongly connected components. The previously discussed algorithm requires two DFS traversals of a Graph. In this post, Tarjan's algorithm is discussed that requires only one DFS traversal:
Tarjan Algorithm is based on the following facts:
- DFS search produces a DFS tree/forest
- Strongly Connected Components form subtrees of the DFS tree.
- If we can find the head of such subtrees, we can print/store all the nodes in that subtree (including the head) and that will be one SCC.
- There is no back edge from one SCC to another (There can be cross edges, but cross edges will not be used while processing the graph).
To find the head of an SCC, we calculate the disc and low array (as done for articulation point, bridge, and biconnected component). As discussed in the previous posts, low[u] indicates the earliest visited vertex (the vertex with minimum discovery time) that can be reached from a subtree rooted with u. A node u is head if disc[u] = low[u]
Below is an illustration of the above approach:

To solve the problem follow the below idea:
Strongly Connected Component relates to directed graph only, but Disc and Low values relate to both directed and undirected graph, so in the above pic we have taken an undirected graph.
In the above Figure, we have shown a graph and one of the DFS trees (There could be different DFS trees on the same graph depending on the order in which edges are traversed). In a DFS tree, continuous arrows are tree edges, and dashed arrows are back edges (DFS Tree Edges ). Disc and Low values are shown in the Figure for every node as (Disc/Low).
Disc: This is the time when a node is visited 1st time while DFS traversal. For nodes A, B, C, .., and J in the DFS tree, Disc values are 1, 2, 3, .., 10.
Low: In the DFS tree, Tree edges take us forward, from the ancestor node to one of its descendants. For example, from node C, tree edges can take us to node G, node I, etc. Back edges take us backward, from a descendant node to one of its ancestors.
For example: From node G, the Back edges take us to E or C. If we look at both the Tree and Back edges together, then we can see that if we start traversal from one node, we may go down the tree via Tree edges and then go up via back edges.
For example, from node E, we can go down to G and then go up to C. Similarly from E, we can go down to I or J and then go up to F. "Low" value of a node tells the topmost reachable ancestor (with minimum possible Disc value) via the subtree of that node. So for any node, a Low value is equal to its Disc value anyway (A node is the ancestor of itself). Then we look into its subtree and see if there is any node that can take us to any of its ancestors.
If there are multiple back edges in the subtree that take us to different ancestors, then we take the one with the minimum Disc value (i.e. the topmost one). If we look at node F, it has two subtrees. Subtree with node G takes us to E and C. The other subtree takes us back to F only. Here topmost ancestor is C where F can reach and so the Low value of F is 3 (The Disc value of C).
Based on the above discussion, it should be clear that the Low values of B, C, and D are 1 (As A is the topmost node where B, C, and D can reach). In the same way, the Low values of E, F, and G are 3, and the Low values of H, I, and J are 6.
For any node u, when DFS starts, Low will be set to its Disc 1st
Then later on DFS will be performed on each of its children v one by one, Low value of u can change in two cases:
- Case1 (Tree Edge): If node v is not visited already, then after the DFS of v is complete, a minimum of low[u] and low[v] will be updated to low[u].
low[u] = min(low[u], low[v]); - Case 2 (Back Edge): When child v is already visited, then a minimum of low[u] and Disc[v] will be updated to low[u].
low[u] = min(low[u], disc[v]);
In case two, can we take low[v] instead of the disc[v] ?? The answer is NO. If you can think why the answer is NO, you probably understood the Low and Disc concept.

Same Low and Disc values help to solve other graph problems like articulation point, bridge, and biconnected component. To track the subtree rooted at the head, we can use a stack (keep pushing the node while visiting). When a head node is found, pop all nodes from the stack till you get the head out of the stack. To make sure, we don't consider cross edges, when we reach a node that is already visited, we should process the visited node only if it is present in the stack, or else ignore the node.
Below is the implementation of Tarjan's algorithm to print all SCCs.
C++
// A C++ program to find strongly connected components in a
// given directed graph using Tarjan's algorithm (single
// DFS)
#include <bits/stdc++.h>
#define NIL -1
using namespace std;
// A class that represents an directed graph
class Graph {
int V; // No. of vertices
list<int>* adj; // A dynamic array of adjacency lists
// A Recursive DFS based function used by SCC()
void SCCUtil(int u, int disc[], int low[],
stack<int>* st, bool stackMember[]);
public:
Graph(int V); // Constructor
void addEdge(int v,
int w); // function to add an edge to graph
void SCC(); // prints strongly connected components
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w) { adj[v].push_back(w); }
// A recursive function that finds and prints strongly
// connected components using DFS traversal u --> The vertex
// to be visited next disc[] --> Stores discovery times of
// visited vertices low[] -- >> earliest visited vertex (the
// vertex with minimum
// discovery time) that can be reached from
// subtree rooted with current vertex
// *st -- >> To store all the connected ancestors (could be
// part
// of SCC)
// stackMember[] --> bit/index array for faster check
// whether
// a node is in stack
void Graph::SCCUtil(int u, int disc[], int low[],
stack<int>* st, bool stackMember[])
{
// A static variable is used for simplicity, we can
// avoid use of static variable by passing a pointer.
static int time = 0;
// Initialize discovery time and low value
disc[u] = low[u] = ++time;
st->push(u);
stackMember[u] = true;
// Go through all vertices adjacent to this
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i) {
int v = *i; // v is current adjacent of 'u'
// If v is not visited yet, then recur for it
if (disc[v] == -1) {
SCCUtil(v, disc, low, st, stackMember);
// Check if the subtree rooted with 'v' has a
// connection to one of the ancestors of 'u'
// Case 1 (per above discussion on Disc and Low
// value)
low[u] = min(low[u], low[v]);
}
// Update low value of 'u' only of 'v' is still in
// stack (i.e. it's a back edge, not cross edge).
// Case 2 (per above discussion on Disc and Low
// value)
else if (stackMember[v] == true)
low[u] = min(low[u], disc[v]);
}
// head node found, pop the stack and print an SCC
int w = 0; // To store stack extracted vertices
if (low[u] == disc[u]) {
while (st->top() != u) {
w = (int)st->top();
cout << w << " ";
stackMember[w] = false;
st->pop();
}
w = (int)st->top();
cout << w << "\n";
stackMember[w] = false;
st->pop();
}
}
// The function to do DFS traversal. It uses SCCUtil()
void Graph::SCC()
{
int* disc = new int[V];
int* low = new int[V];
bool* stackMember = new bool[V];
stack<int>* st = new stack<int>();
// Initialize disc and low, and stackMember arrays
for (int i = 0; i < V; i++) {
disc[i] = NIL;
low[i] = NIL;
stackMember[i] = false;
}
// Call the recursive helper function to find strongly
// connected components in DFS tree with vertex 'i'
for (int i = 0; i < V; i++)
if (disc[i] == NIL)
SCCUtil(i, disc, low, st, stackMember);
}
// Driver program to test above function
int main()
{
cout << "\nSCCs in first graph \n";
Graph g1(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.SCC();
cout << "\nSCCs in second graph \n";
Graph g2(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.SCC();
cout << "\nSCCs in third graph \n";
Graph g3(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.SCC();
cout << "\nSCCs in fourth graph \n";
Graph g4(11);
g4.addEdge(0, 1);
g4.addEdge(0, 3);
g4.addEdge(1, 2);
g4.addEdge(1, 4);
g4.addEdge(2, 0);
g4.addEdge(2, 6);
g4.addEdge(3, 2);
g4.addEdge(4, 5);
g4.addEdge(4, 6);
g4.addEdge(5, 6);
g4.addEdge(5, 7);
g4.addEdge(5, 8);
g4.addEdge(5, 9);
g4.addEdge(6, 4);
g4.addEdge(7, 9);
g4.addEdge(8, 9);
g4.addEdge(9, 8);
g4.SCC();
cout << "\nSCCs in fifth graph \n";
Graph g5(5);
g5.addEdge(0, 1);
g5.addEdge(1, 2);
g5.addEdge(2, 3);
g5.addEdge(2, 4);
g5.addEdge(3, 0);
g5.addEdge(4, 2);
g5.SCC();
return 0;
}
// Java program to find strongly connected
// components in a given directed graph
// using Tarjan's algorithm (single DFS)
import java.io.*;
import java.util.*;
// This class represents a directed graph
// using adjacency list representation
class Graph {
// No. of vertices
private int V;
// Adjacency Lists
private LinkedList<Integer> adj[];
private int Time;
// Constructor
@SuppressWarnings("unchecked") Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList();
Time = 0;
}
// Function to add an edge into the graph
void addEdge(int v, int w) { adj[v].add(w); }
// A recursive function that finds and prints strongly
// connected components using DFS traversal
// u --> The vertex to be visited next
// disc[] --> Stores discovery times of visited vertices
// low[] -- >> earliest visited vertex (the vertex with
// minimum discovery time) that can be
// reached from subtree rooted with current
// vertex
// st -- >> To store all the connected ancestors (could
// be part
// of SCC)
// stackMember[] --> bit/index array for faster check
// whether a node is in stack
void SCCUtil(int u, int low[], int disc[],
boolean stackMember[], Stack<Integer> st)
{
// Initialize discovery time and low value
disc[u] = Time;
low[u] = Time;
Time += 1;
stackMember[u] = true;
st.push(u);
int n;
// Go through all vertices adjacent to this
Iterator<Integer> i = adj[u].iterator();
while (i.hasNext()) {
n = i.next();
if (disc[n] == -1) {
SCCUtil(n, low, disc, stackMember, st);
// Check if the subtree rooted with v
// has a connection to one of the
// ancestors of u
// Case 1 (per above discussion on
// Disc and Low value)
low[u] = Math.min(low[u], low[n]);
}
else if (stackMember[n] == true) {
// Update low value of 'u' only if 'v' is
// still in stack (i.e. it's a back edge,
// not cross edge).
// Case 2 (per above discussion on Disc
// and Low value)
low[u] = Math.min(low[u], disc[n]);
}
}
// head node found, pop the stack and print an SCC
// To store stack extracted vertices
int w = -1;
if (low[u] == disc[u]) {
while (w != u) {
w = (int)st.pop();
System.out.print(w + " ");
stackMember[w] = false;
}
System.out.println();
}
}
// The function to do DFS traversal.
// It uses SCCUtil()
void SCC()
{
// Mark all the vertices as not visited
// and Initialize parent and visited,
// and ap(articulation point) arrays
int disc[] = new int[V];
int low[] = new int[V];
for (int i = 0; i < V; i++) {
disc[i] = -1;
low[i] = -1;
}
boolean stackMember[] = new boolean[V];
Stack<Integer> st = new Stack<Integer>();
// Call the recursive helper function
// to find articulation points
// in DFS tree rooted with vertex 'i'
for (int i = 0; i < V; i++) {
if (disc[i] == -1)
SCCUtil(i, low, disc, stackMember, st);
}
}
// Driver code
public static void main(String args[])
{
// Create a graph given in the above diagram
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
System.out.println("SSC in first graph ");
g1.SCC();
Graph g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
System.out.println("\nSSC in second graph ");
g2.SCC();
Graph g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
System.out.println("\nSSC in third graph ");
g3.SCC();
Graph g4 = new Graph(11);
g4.addEdge(0, 1);
g4.addEdge(0, 3);
g4.addEdge(1, 2);
g4.addEdge(1, 4);
g4.addEdge(2, 0);
g4.addEdge(2, 6);
g4.addEdge(3, 2);
g4.addEdge(4, 5);
g4.addEdge(4, 6);
g4.addEdge(5, 6);
g4.addEdge(5, 7);
g4.addEdge(5, 8);
g4.addEdge(5, 9);
g4.addEdge(6, 4);
g4.addEdge(7, 9);
g4.addEdge(8, 9);
g4.addEdge(9, 8);
System.out.println("\nSSC in fourth graph ");
g4.SCC();
Graph g5 = new Graph(5);
g5.addEdge(0, 1);
g5.addEdge(1, 2);
g5.addEdge(2, 3);
g5.addEdge(2, 4);
g5.addEdge(3, 0);
g5.addEdge(4, 2);
System.out.println("\nSSC in fifth graph ");
g5.SCC();
}
}
// This code is contributed by
// Prateek Gupta (@prateekgupta10)
# Python program to find strongly connected components in a given
# directed graph using Tarjan's algorithm (single DFS)
#Complexity : O(V+E)
from collections import defaultdict
# This class represents an directed graph
# using adjacency list representation
class Graph:
def __init__(self, vertices):
# No. of vertices
self.V = vertices
# default dictionary to store graph
self.graph = defaultdict(list)
self.Time = 0
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
'''A recursive function that find finds and prints strongly connected
components using DFS traversal
u --> The vertex to be visited next
disc[] --> Stores discovery times of visited vertices
low[] -- >> earliest visited vertex (the vertex with minimum
discovery time) that can be reached from subtree
rooted with current vertex
st -- >> To store all the connected ancestors (could be part
of SCC)
stackMember[] --> bit/index array for faster check whether
a node is in stack
'''
def SCCUtil(self, u, low, disc, stackMember, st):
# Initialize discovery time and low value
disc[u] = self.Time
low[u] = self.Time
self.Time += 1
stackMember[u] = True
st.append(u)
# Go through all vertices adjacent to this
for v in self.graph[u]:
# If v is not visited yet, then recur for it
if disc[v] == -1:
self.SCCUtil(v, low, disc, stackMember, st)
# Check if the subtree rooted with v has a connection to
# one of the ancestors of u
# Case 1 (per above discussion on Disc and Low value)
low[u] = min(low[u], low[v])
elif stackMember[v] == True:
'''Update low value of 'u' only if 'v' is still in stack
(i.e. it's a back edge, not cross edge).
Case 2 (per above discussion on Disc and Low value) '''
low[u] = min(low[u], disc[v])
# head node found, pop the stack and print an SCC
w = -1 # To store stack extracted vertices
if low[u] == disc[u]:
while w != u:
w = st.pop()
print(w, end=" ")
stackMember[w] = False
print()
# The function to do DFS traversal.
# It uses recursive SCCUtil()
def SCC(self):
# Mark all the vertices as not visited
# and Initialize parent and visited,
# and ap(articulation point) arrays
disc = [-1] * (self.V)
low = [-1] * (self.V)
stackMember = [False] * (self.V)
st = []
# Call the recursive helper function
# to find articulation points
# in DFS tree rooted with vertex 'i'
for i in range(self.V):
if disc[i] == -1:
self.SCCUtil(i, low, disc, stackMember, st)
# Create a graph given in the above diagram
g1 = Graph(5)
g1.addEdge(1, 0)
g1.addEdge(0, 2)
g1.addEdge(2, 1)
g1.addEdge(0, 3)
g1.addEdge(3, 4)
print("SSC in first graph ")
g1.SCC()
g2 = Graph(4)
g2.addEdge(0, 1)
g2.addEdge(1, 2)
g2.addEdge(2, 3)
print("\nSSC in second graph ")
g2.SCC()
g3 = Graph(7)
g3.addEdge(0, 1)
g3.addEdge(1, 2)
g3.addEdge(2, 0)
g3.addEdge(1, 3)
g3.addEdge(1, 4)
g3.addEdge(1, 6)
g3.addEdge(3, 5)
g3.addEdge(4, 5)
print("\nSSC in third graph ")
g3.SCC()
g4 = Graph(11)
g4.addEdge(0, 1)
g4.addEdge(0, 3)
g4.addEdge(1, 2)
g4.addEdge(1, 4)
g4.addEdge(2, 0)
g4.addEdge(2, 6)
g4.addEdge(3, 2)
g4.addEdge(4, 5)
g4.addEdge(4, 6)
g4.addEdge(5, 6)
g4.addEdge(5, 7)
g4.addEdge(5, 8)
g4.addEdge(5, 9)
g4.addEdge(6, 4)
g4.addEdge(7, 9)
g4.addEdge(8, 9)
g4.addEdge(9, 8)
print("\nSSC in fourth graph ")
g4.SCC()
g5 = Graph(5)
g5.addEdge(0, 1)
g5.addEdge(1, 2)
g5.addEdge(2, 3)
g5.addEdge(2, 4)
g5.addEdge(3, 0)
g5.addEdge(4, 2)
print("\nSSC in fifth graph ")
g5.SCC()
# This code is contributed by Neelam Yadav
<script>
// Javascript program to find strongly connected
// components in a given directed graph
// using Tarjan's algorithm (single DFS)
// This class represents a directed graph
// using adjacency list representation
class Graph{
// Constructor
constructor(v)
{
this.V = v;
this.adj = new Array(v);
for(let i = 0; i < v; ++i)
this.adj[i] = [];
this.Time = 0;
}
// Function to add an edge into the graph
addEdge(v, w)
{
this.adj[v].push(w);
}
// A recursive function that finds and prints strongly
// connected components using DFS traversal
// u --> The vertex to be visited next
// disc[] --> Stores discovery times of visited vertices
// low[] -- >> earliest visited vertex (the vertex with
// minimum discovery time) that can be reached
// from subtree rooted with current vertex
// st -- >> To store all the connected ancestors (could be
// part of SCC)
// stackMember[] --> bit/index array for faster check
// whether a node is in stack
SCCUtil(u, low, disc, stackMember, st)
{
// Initialize discovery time and low value
disc[u] = this.Time;
low[u] = this.Time;
this.Time += 1;
stackMember[u] = true;
st.push(u);
let n;
// Go through all vertices adjacent to this
for(let i of this.adj[u])
{
n = i;
if (disc[n] == -1)
{
this.SCCUtil(n, low, disc, stackMember, st);
// Check if the subtree rooted with v
// has a connection to one of the
// ancestors of u
// Case 1 (per above discussion on
// Disc and Low value)
low[u] = Math.min(low[u], low[n]);
}
else if (stackMember[n] == true)
{
// Update low value of 'u' only if 'v' is
// still in stack (i.e. it's a back edge,
// not cross edge).
// Case 2 (per above discussion on Disc
// and Low value)
low[u] = Math.min(low[u], disc[n]);
}
}
// Head node found, pop the stack and print an SCC
// To store stack extracted vertices
let w = -1;
if (low[u] == disc[u])
{
while (w != u)
{
w = st.pop();
document.write(w + " ");
stackMember[w] = false;
}
document.write("<br>");
}
}
// The function to do DFS traversal.
// It uses SCCUtil()
SCC()
{
// Mark all the vertices as not visited
// and Initialize parent and visited,
// and ap(articulation point) arrays
let disc = new Array(this.V);
let low = new Array(this.V);
for(let i = 0;i < this.V; i++)
{
disc[i] = -1;
low[i] = -1;
}
let stackMember = new Array(this.V);
let st = [];
// Call the recursive helper function
// to find articulation points
// in DFS tree rooted with vertex 'i'
for(let i = 0; i < this.V; i++)
{
if (disc[i] == -1)
this.SCCUtil(i, low, disc,
stackMember, st);
}
}
}
// Driver code
// Create a graph given in the above diagram
let g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
document.write("SSC in first graph <br>");
g1.SCC();
let g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
document.write("\nSSC in second graph<br> ");
g2.SCC();
let g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
document.write("\nSSC in third graph <br>");
g3.SCC();
let g4 = new Graph(11);
g4.addEdge(0, 1);
g4.addEdge(0, 3);
g4.addEdge(1, 2);
g4.addEdge(1, 4);
g4.addEdge(2, 0);
g4.addEdge(2, 6);
g4.addEdge(3, 2);
g4.addEdge(4, 5);
g4.addEdge(4, 6);
g4.addEdge(5, 6);
g4.addEdge(5, 7);
g4.addEdge(5, 8);
g4.addEdge(5, 9);
g4.addEdge(6, 4);
g4.addEdge(7, 9);
g4.addEdge(8, 9);
g4.addEdge(9, 8);
document.write("\nSSC in fourth graph<br> ");
g4.SCC();
let g5 = new Graph (5);
g5.addEdge(0, 1);
g5.addEdge(1, 2);
g5.addEdge(2, 3);
g5.addEdge(2, 4);
g5.addEdge(3, 0);
g5.addEdge(4, 2);
document.write("\nSSC in fifth graph <br>");
g5.SCC();
// This code is contributed by avanitrachhadiya2155
</script>
using System;
using System.Collections.Generic;
// This class represents a directed graph
// using adjacency list representation
class Graph
{
// No. of vertices
private int V;
// Adjacency Lists
private List<int>[] adj;
private int Time;
// Constructor
public Graph(int v)
{
V = v;
adj = new List<int>[v];
for (int i = 0; i < v; ++i)
adj[i] = new List<int>();
Time = 0;
}
// Function to add an edge into the graph
public void addEdge(int v, int w) { adj[v].Add(w); }
// A recursive function that finds and prints strongly
// connected components using DFS traversal
// u --> The vertex to be visited next
// disc[] --> Stores discovery times of visited vertices
// low[] -- >> earliest visited vertex (the vertex with
// minimum discovery time) that can be
// reached from subtree rooted with current
// vertex
// st -- >> To store all the connected ancestors (could
// be part
// of SCC)
// stackMember[] --> bit/index array for faster check
// whether a node is in stack
private void SCCUtil(int u, int[] low, int[] disc,
bool[] stackMember, Stack<int> st)
{
// Initialize discovery time and low value
disc[u] = Time;
low[u] = Time;
Time += 1;
stackMember[u] = true;
st.Push(u);
int n;
// Go through all vertices adjacent to this
foreach (int i in adj[u])
{
n = i;
if (disc[n] == -1)
{
SCCUtil(n, low, disc, stackMember, st);
// Check if the subtree rooted with v
// has a connection to one of the
// ancestors of u
// Case 1 (per above discussion on
// Disc and Low value)
low[u] = Math.Min(low[u], low[n]);
}
else if (stackMember[n] == true)
{
// Update low value of 'u' only if 'v' is
// still in stack (i.e. it's a back edge,
// not cross edge).
// Case 2 (per above discussion on Disc
// and Low value)
low[u] = Math.Min(low[u], disc[n]);
}
}
// head node found, pop the stack and print an SCC
// To store stack extracted vertices
int w = -1;
if (low[u] == disc[u])
{
while (w != u)
{
w = st.Pop();
Console.Write(w + " ");
stackMember[w] = false;
}
Console.WriteLine();
}
}
// The function to do DFS traversal.
// It uses SCCUtil()
public void SCC()
{
// Mark all the vertices as not visited
// and Initialize parent and visited,
// and ap(articulation point) arrays
int[] disc = new int[V];
int[] low = new int[V];
for (int i = 0; i < V; i++)
{
disc[i] = -1;
low[i] = -1;
}
bool[] stackMember = new bool[V];
Stack<int> st = new Stack<int>();
// Call the recursive helper function
// to find strongly connected components
for (int i = 0; i < V; i++)
if (disc[i] == -1)
SCCUtil(i, low, disc, stackMember, st);
}
static void Main(string[] args)
{
// Create a new graph with 5 vertices
Graph g = new Graph(5);
// Add edges to the graph
g.addEdge(1, 0);
g.addEdge(0, 2);
g.addEdge(2, 1);
g.addEdge(0, 3);
g.addEdge(3, 4);
Console.WriteLine("Strongly Connected Components:");
g.SCC();
Graph g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
Console.WriteLine("\nSSC in second graph ");
g2.SCC();
Graph g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
Console.WriteLine("\nSSC in third graph ");
g3.SCC();
Graph g4 = new Graph(11);
g4.addEdge(0, 1);
g4.addEdge(0, 3);
g4.addEdge(1, 2);
g4.addEdge(1, 4);
g4.addEdge(2, 0);
g4.addEdge(2, 6);
g4.addEdge(3, 2);
g4.addEdge(4, 5);
g4.addEdge(4, 6);
g4.addEdge(5, 6);
g4.addEdge(5, 7);
g4.addEdge(5, 8);
g4.addEdge(5, 9);
g4.addEdge(6, 4);
g4.addEdge(7, 9);
g4.addEdge(8, 9);
g4.addEdge(9, 8);
Console.WriteLine("\nSSC in fourth graph ");
g4.SCC();
Graph g5 = new Graph(5);
g5.addEdge(0, 1);
g5.addEdge(1, 2);
g5.addEdge(2, 3);
g5.addEdge(2, 4);
g5.addEdge(3, 0);
g5.addEdge(4, 2);
Console.WriteLine("\nSSC in fifth graph ");
g5.SCC();
}
}
OutputSCCs in first graph
4
3
1 2 0
SCCs in second graph
3
2
1
0
SCCs in third graph
5
3
4
6
2 1 0
SCCs in fourth graph
8 9
7
5 4 6
3 2 1 0
10
SCCs in fifth graph
4 3 2 1 0
Time Complexity: The above algorithm mainly calls DFS, DFS takes O(V+E) for a graph represented using an adjacency list.
Auxiliary Space: O(V)
Similar Reads
Graph Algorithms Graph algorithms are methods used to manipulate and analyze graphs, solving various range of problems like finding the shortest path, cycles detection. If you are looking for difficulty-wise list of problems, please refer to Graph Data Structure.BasicsGraph and its representationsBFS and DFS Breadth
3 min read
Introduction to Graph Data Structure Graph Data Structure is a non-linear data structure consisting of vertices and edges. It is useful in fields such as social network analysis, recommendation systems, and computer networks. In the field of sports data science, graph data structure can be used to analyze and understand the dynamics of
15+ min read
Graph and its representations A Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is den
12 min read
Types of Graphs with Examples A graph is a mathematical structure that represents relationships between objects by connecting a set of points. It is used to establish a pairwise relationship between elements in a given set. graphs are widely used in discrete mathematics, computer science, and network theory to represent relation
9 min read
Basic Properties of a Graph A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. The basic properties of a graph include: Vertices (nodes): The points where edges meet in a graph are kn
4 min read
Applications, Advantages and Disadvantages of Graph Graph is a non-linear data structure that contains nodes (vertices) and edges. A graph is a collection of set of vertices and edges (formed by connecting two vertices). A graph is defined as G = {V, E} where V is the set of vertices and E is the set of edges. Graphs can be used to model a wide varie
7 min read
Transpose graph Transpose of a directed graph G is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in G. That is, if G contains an edge (u, v) then the converse/transpose/reverse of G contains an edge (v, u) and vice versa. Giv
9 min read
Difference Between Graph and Tree Graphs and trees are two fundamental data structures used in computer science to represent relationships between objects. While they share some similarities, they also have distinct differences that make them suitable for different applications. Difference Between Graph and Tree What is Graph?A grap
2 min read
BFS and DFS on Graph
Breadth First Search or BFS for a GraphGiven a undirected graph represented by an adjacency list adj, where each adj[i] represents the list of vertices connected to vertex i. Perform a Breadth First Search (BFS) traversal starting from vertex 0, visiting vertices from left to right according to the adjacency list, and return a list conta
15+ min read
Depth First Search or DFS for a GraphIn Depth First Search (or DFS) for a graph, we traverse all adjacent vertices one by one. When we traverse an adjacent vertex, we completely finish the traversal of all vertices reachable through that adjacent vertex. This is similar to a tree, where we first completely traverse the left subtree and
13 min read
Applications, Advantages and Disadvantages of Depth First Search (DFS)Depth First Search is a widely used algorithm for traversing a graph. Here we have discussed some applications, advantages, and disadvantages of the algorithm. Applications of Depth First Search:1. Detecting cycle in a graph: A graph has a cycle if and only if we see a back edge during DFS. So we ca
4 min read
Applications, Advantages and Disadvantages of Breadth First Search (BFS)We have earlier discussed Breadth First Traversal Algorithm for Graphs. Here in this article, we will see the applications, advantages, and disadvantages of the Breadth First Search. Applications of Breadth First Search: 1. Shortest Path and Minimum Spanning Tree for unweighted graph: In an unweight
4 min read
Iterative Depth First Traversal of GraphGiven a directed Graph, the task is to perform Depth First Search of the given graph.Note: Start DFS from node 0, and traverse the nodes in the same order as adjacency list.Note : There can be multiple DFS traversals of a graph according to the order in which we pick adjacent vertices. Here we pick
10 min read
BFS for Disconnected GraphIn the previous post, BFS only with a particular vertex is performed i.e. it is assumed that all vertices are reachable from the starting vertex. But in the case of a disconnected graph or any vertex that is unreachable from all vertex, the previous implementation will not give the desired output, s
14 min read
Transitive Closure of a Graph using DFSGiven a directed graph, find out if a vertex v is reachable from another vertex u for all vertex pairs (u, v) in the given graph. Here reachable means that there is a path from vertex u to v. The reach-ability matrix is called transitive closure of a graph. For example, consider below graph: GraphTr
8 min read
Difference between BFS and DFSBreadth-First Search (BFS) and Depth-First Search (DFS) are two fundamental algorithms used for traversing or searching graphs and trees. This article covers the basic difference between Breadth-First Search and Depth-First Search.Difference between BFS and DFSParametersBFSDFSStands forBFS stands fo
2 min read
Cycle in a Graph
Detect Cycle in a Directed GraphGiven the number of vertices V and a list of directed edges, determine whether the graph contains a cycle or not.Examples: Input: V = 4, edges[][] = [[0, 1], [0, 2], [1, 2], [2, 0], [2, 3]]Cycle: 0 → 2 → 0 Output: trueExplanation: The diagram clearly shows a cycle 0 → 2 → 0 Input: V = 4, edges[][] =
15+ min read
Detect cycle in an undirected graphGiven an undirected graph, the task is to check if there is a cycle in the given graph.Examples:Input: V = 4, edges[][]= [[0, 1], [0, 2], [1, 2], [2, 3]]Undirected Graph with 4 vertices and 4 edgesOutput: trueExplanation: The diagram clearly shows a cycle 0 → 2 → 1 → 0Input: V = 4, edges[][] = [[0,
8 min read
Detect Cycle in a directed graph using colorsGiven a directed graph represented by the number of vertices V and a list of directed edges, determine whether the graph contains a cycle.Your task is to implement a function that accepts V (number of vertices) and edges (an array of directed edges where each edge is a pair [u, v]), and returns true
9 min read
Detect a negative cycle in a Graph | (Bellman Ford)Given a directed weighted graph, your task is to find whether the given graph contains any negative cycles that are reachable from the source vertex (e.g., node 0).Note: A negative-weight cycle is a cycle in a graph whose edges sum to a negative value.Example:Input: V = 4, edges[][] = [[0, 3, 6], [1
15+ min read
Cycles of length n in an undirected and connected graphGiven an undirected and connected graph and a number n, count the total number of simple cycles of length n in the graph. A simple cycle of length n is defined as a cycle that contains exactly n vertices and n edges. Note that for an undirected graph, each cycle should only be counted once, regardle
10 min read
Detecting negative cycle using Floyd WarshallWe are given a directed graph. We need compute whether the graph has negative cycle or not. A negative cycle is one in which the overall sum of the cycle comes negative. Negative weights are found in various applications of graphs. For example, instead of paying cost for a path, we may get some adva
12 min read
Clone a Directed Acyclic GraphA directed acyclic graph (DAG) is a graph which doesn't contain a cycle and has directed edges. We are given a DAG, we need to clone it, i.e., create another graph that has copy of its vertices and edges connecting them. Examples: Input : 0 - - - > 1 - - - -> 4 | / \ ^ | / \ | | / \ | | / \ |
12 min read