Reverse zigzag Traversal of a Binary Tree
Last Updated :
21 Oct, 2024
Given a Binary Tree, the task is to print the Reverse Zig-zag order of the tree. In Zig-zag traversal starting from the first level go from left to right for odd-numbered levels and right to left for even-numbered levels. For Reverse Zig-zag traversal just print the reverse of this traversal.
Examples:
Input:
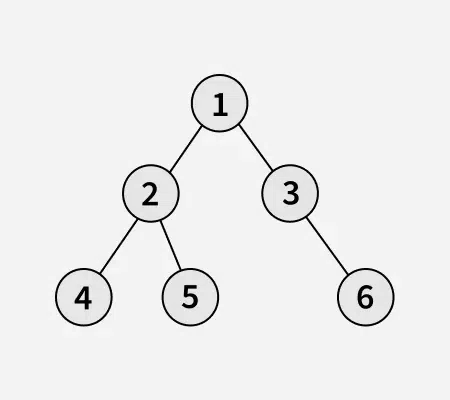
Output: 6 5 4 2 3 1
Explanation: The Zig-zag traversal is: 1 (left to right), then 3 2 (right to left), followed by 4 5 6 (left to right). The reverse of this is 6 5 4 2 3 1.

Approach:
The idea is to traverse the tree in a Reverse Level Order manner but with a slight modification. We will use a variable flag and initially set it's value to one. As we complete the reverse level order traversal of the tree, from right to left we will set the value of flag to zero, so that next time we traverse the Tree from left to right and as we complete the traversal we set it's value back to one. We will repeat this whole step until we have traversed the Binary Tree completely.
Below is the implementation of the above approach:
C++
// C++ implementation for printing reverse zig-zag
// order of a Binary Tree
#include <iostream>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int x) {
data = x;
left = nullptr;
right = nullptr;
}
};
// Recursive function to find height of binary tree
int Height(Node* root) {
if (root == nullptr)
return 0;
// Compute the height of each subtree
int lheight = Height(root->left);
int rheight = Height(root->right);
// Return the maximum of two
return max(lheight + 1, rheight + 1);
}
// Function to print nodes from right to left
void PrintRight(Node* root, int level) {
if (root == nullptr)
return;
if (level == 1)
cout << root->data << " ";
else if (level > 1) {
PrintRight(root->right, level - 1);
PrintRight(root->left, level - 1);
}
}
// Function to print nodes from left to right
void PrintLeft(Node* root, int level) {
if (root == nullptr)
return;
if (level == 1)
cout << root->data << " ";
else if (level > 1) {
PrintLeft(root->left, level - 1);
PrintLeft(root->right, level - 1);
}
}
// Function to print reverse zig-zag of a Binary tree
void PrintReverseZigzag(Node* root) {
// Flag is used to mark the change in level
int flag = 1;
// Height of the tree
int height = Height(root);
for (int i = height; i >= 1; i--) {
// If flag value is one, print nodes
// from right to left
if (flag == 1) {
PrintRight(root, i);
// Mark flag as zero to traverse
// from left to right next
flag = 0;
}
// If flag is zero, print nodes from
// left to right
else if (flag == 0) {
PrintLeft(root, i);
// Mark flag as one to traverse
// from right to left next
flag = 1;
}
}
}
int main() {
// Representation of the binary tree
// 1
// / \
// 2 3
// / \ \
// 4 5 6
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->right = new Node(6);
PrintReverseZigzag(root);
return 0;
}
// Java implementation for printing reverse zig-zag
// order of a Binary Tree
class Node {
int data;
Node left;
Node right;
Node(int x) {
data = x;
left = null;
right = null;
}
}
// Class to implement reverse zig-zag traversal
public class GfG {
// Recursive function to find height of binary tree
static int height(Node root) {
if (root == null)
return 0;
// Compute the height of each subtree
int lheight = height(root.left);
int rheight = height(root.right);
// Return the maximum of two
return Math.max(lheight + 1, rheight + 1);
}
// Function to print nodes from right to left
static void printRight(Node root, int level) {
if (root == null)
return;
if (level == 1)
System.out.print(root.data + " ");
else if (level > 1) {
printRight(root.right, level - 1);
printRight(root.left, level - 1);
}
}
// Function to print nodes from left to right
static void printLeft(Node root, int level) {
if (root == null)
return;
if (level == 1)
System.out.print(root.data + " ");
else if (level > 1) {
printLeft(root.left, level - 1);
printLeft(root.right, level - 1);
}
}
// Function to print reverse zig-zag of a Binary tree
static void printReverseZigzag(Node root) {
// Flag is used to mark the change in level
int flag = 1;
// Height of the tree
int height = height(root);
for (int i = height; i >= 1; i--) {
// If flag value is one, print
// nodes from right to left
if (flag == 1) {
printRight(root, i);
// Mark flag as zero to traverse
// from left to right next
flag = 0;
}
// If flag is zero, print nodes from left to right
else {
printLeft(root, i);
// Mark flag as one to traverse
// from right to left next
flag = 1;
}
}
}
public static void main(String[] args) {
// Representation of the binary tree
// 1
// / \
// 2 3
// / \ \
// 4 5 6
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
printReverseZigzag(root);
}
}
# Python implementation for printing reverse zig-zag
# order of a Binary Tree
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
# Function to find height of binary tree
def height(root):
if root is None:
return 0
# Compute the height of each subtree
lheight = height(root.left)
rheight = height(root.right)
# Return the maximum of two
return max(lheight + 1, rheight + 1)
# Function to print nodes from right to left
def print_right(root, level):
if root is None:
return
if level == 1:
print(root.data, end=' ')
elif level > 1:
print_right(root.right, level - 1)
print_right(root.left, level - 1)
# Function to print nodes from left to right
def print_left(root, level):
if root is None:
return
if level == 1:
print(root.data, end=' ')
elif level > 1:
print_left(root.left, level - 1)
print_left(root.right, level - 1)
# Function to print reverse zig-zag of a Binary tree
def print_reverse_zigzag(root):
# Flag is used to mark the change in level
flag = 1
# Height of the tree
h = height(root)
for i in range(h, 0, -1):
# If flag value is one, print nodes from right to left
if flag == 1:
print_right(root, i)
# Mark flag as zero to traverse from left to right next
flag = 0
# If flag is zero, print nodes from left to right
else:
print_left(root, i)
# Mark flag as one to traverse from right to left next
flag = 1
if __name__ == "__main__":
# Representation of the binary tree
# 1
# / \
# 2 3
# / \ \
# 4 5 6
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.right = Node(6)
print_reverse_zigzag(root)
// C# implementation for printing reverse zig-zag
// order of a Binary Tree
using System;
class Node {
public int data;
public Node left;
public Node right;
public Node(int x) {
data = x;
left = null;
right = null;
}
}
class GfG {
// Recursive function to find height of binary tree
static int Height(Node root) {
if (root == null)
return 0;
// Compute the height of each subtree
int lheight = Height(root.left);
int rheight = Height(root.right);
// Return the maximum of two
return Math.Max(lheight + 1, rheight + 1);
}
// Function to print nodes from right to left
static void PrintRight(Node root, int level) {
if (root == null)
return;
if (level == 1)
Console.Write(root.data + " ");
else if (level > 1) {
PrintRight(root.right, level - 1);
PrintRight(root.left, level - 1);
}
}
// Function to print nodes from left to right
static void PrintLeft(Node root, int level) {
if (root == null)
return;
if (level == 1)
Console.Write(root.data + " ");
else if (level > 1) {
PrintLeft(root.left, level - 1);
PrintLeft(root.right, level - 1);
}
}
// Function to print reverse zig-zag of a Binary tree
static void PrintReverseZigzag(Node root) {
// Flag is used to mark the change in level
int flag = 1;
// Height of the tree
int height = Height(root);
for (int i = height; i >= 1; i--) {
// If flag value is one, print nodes from
// right to left
if (flag == 1) {
PrintRight(root, i);
// Mark flag as zero to traverse from
// left to right next
flag = 0;
}
// If flag is zero, print nodes from left to right
else {
PrintLeft(root, i);
// Mark flag as one to traverse from
// right to left next
flag = 1;
}
}
}
public static void Main() {
// Representation of the binary tree
// 1
// / \
// 2 3
// / \ \
// 4 5 6
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
PrintReverseZigzag(root);
}
}
// JavaScript implementation for printing reverse zig-zag
// order of a Binary Tree
class Node {
constructor(x) {
this.data = x;
this.left = null;
this.right = null;
}
}
// Recursive function to find height of binary tree
function height(root) {
if (root === null)
return 0;
// Compute the height of each subtree
let lheight = height(root.left);
let rheight = height(root.right);
// Return the maximum of two
return Math.max(lheight + 1, rheight + 1);
}
// Function to print nodes from right to left
function printRight(root, level) {
if (root === null)
return;
if (level === 1)
console.log(root.data + " ");
else if (level > 1) {
printRight(root.right, level - 1);
printRight(root.left, level - 1);
}
}
// Function to print nodes from left to right
function printLeft(root, level) {
if (root === null)
return;
if (level === 1)
console.log(root.data + " ");
else if (level > 1) {
printLeft(root.left, level - 1);
printLeft(root.right, level - 1);
}
}
// Function to print reverse zig-zag of a Binary tree
function printReverseZigzag(root) {
// Flag is used to mark the change in level
let flag = 1;
// Height of the tree
let h = height(root);
for (let i = h; i >= 1; i--) {
// If flag value is one, print nodes
// from right to left
if (flag === 1) {
printRight(root, i);
// Mark flag as zero to traverse from
// left to right next
flag = 0;
}
// If flag is zero, print nodes from
// left to right
else {
printLeft(root, i);
// Mark flag as one to traverse from
// right to left next
flag = 1;
}
}
}
// Representation of the binary tree
// 1
// / \
// 2 3
// / \ \
// 4 5 6
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
printReverseZigzag(root);
Time Complexity: O(n), where n is the number of nodes in the binary tree, as each node is visited once.
Auxiliary Space: O(h), where h is the height of the tree, due to the recursive call stack used during traversal.
Similar Reads
Triple Order Traversal of a Binary Tree Given a Binary Tree, the task is to find its Triple Order Traversal. Triple Order Traversal is a tree traversal technique in which every node is traversed thrice in the following order: Visit the root nodeTraverse the left subtreeVisit the root nodeTraverse the right subtreeVisit the root node.Examp
7 min read
ZigZag Level Order Traversal of an N-ary Tree Given a Generic Tree consisting of n nodes, the task is to find the ZigZag Level Order Traversal of the given tree.Note: A generic tree is a tree where each node can have zero or more children nodes. Unlike a binary tree, which has at most two children per node (left and right), a generic tree allow
8 min read
Vertical Traversal of a Binary Tree Given a Binary Tree, the task is to find its vertical traversal starting from the leftmost level to the rightmost level. If multiple nodes pass through a vertical line, they should be printed as they appear in the level order traversal of the tree.Examples: Input:Output: [[4], [2], [1, 5, 6], [3, 8]
10 min read
Double Order Traversal of a Binary Tree Given a Binary Tree, the task is to find its Double Order Traversal. Double Order Traversal is a tree traversal technique in which every node is traversed twice in the following order: Visit the Node.Traverse the Left Subtree.Visit the Node.Traverse the Right Subtree.Examples:Input: Output: 1 7 4 4
6 min read
Reverse Clockwise spiral traversal of a binary tree Given a Binary Tree. The task is to print the circular reverse clockwise spiral order traversal of the given binary tree.Reverse Clockwise Traversal means to traverse the tree in clockwise direction spirally starting from the bottom instead of top root node.Examples: Input : 1 / \ 2 3 / \ \ 4 5 6 /
11 min read