Types of Graphs with Examples

A graph is a mathematical structure that represents relationships between objects by connecting a set of points. It is used to establish a pairwise relationship between elements in a given set. graphs are widely used in discrete mathematics, computer science, and network theory to represent relationships between objects.

The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. More formally a graph consists of vertices (nodes) connected by edges (lines). These edges define the relationships between the vertices. Formally, a graph G is represented as:

G = (V, E)

where:

• V is the set of vertices (nodes).
• E is the set of edges (connections) between pairs of vertices.

Types of Graphs

1. Finite Graphs

A graph is said to be finite if it has a finite number of vertices and a finite number of edges. A finite graph is a graph with a finite number of vertices and edges. In other words, both the number of vertices and the number of edges in a finite graph are limited and can be counted. Finite graphs are used to represent real-world situations where there are a limited number of objects and their connections. They help in organizing, analyzing, and optimizing relationships in different applications.

2. Infinite Graph: 

A graph is called an infinite graph if it has an infinite number of vertices and an infinite number of edges. Unlike finite graphs, which have a fixed number of nodes and connections, infinite graphs extend indefinitely.

3. Trivial Graph

A graph is said to be trivial if a finite graph contains only one vertex and no edge. A trivial graph is a graph with only one vertex and no edges. It is also known as a singleton graph or a single vertex graph. A trivial graph is the simplest type of graph and is often used as a starting point for building more complex graphs. In graph theory, trivial graphs are considered to be a degenerate case and are not typically studied in detail

4. Simple Graph

A simple graph is a graph that does not contain more than one edge between the pair of vertices. A simple railway track connecting different cities is an example of a simple graph. 

5. Multi Graph

Any graph which contains some parallel edges but doesn’t contain any self-loop is called a multigraph. For example a Road Map. 

• Parallel Edges: If two vertices are connected with more than one edge then such edges are called parallel edges that are many routes but one destination.
• Loop: An edge of a graph that starts from a vertex and ends at the same vertex is called a loop or a self-loop.

6. Null Graph

A graph of order n and size zero is a graph where there are only isolated vertices with no edges connecting any pair of vertices.A null graph is a graph with no edges. In other words, it is a graph with only vertices and no connections between them. A null graph can also be referred to as an edgeless graph, an isolated graph, or a discrete graph

7. Complete Graph

A simple graph with n vertices is called a complete graph if the degree of each vertex is n-1, that is, one vertex is attached with n-1 edges or the rest of the vertices in the graph. A complete graph is also called Full Graph. 

8.Directed Graphs:

A graph in which edges have a direction, i.e., the edges have arrows indicating the direction of traversal.

9. Undirected Graphs

An undirected graph is a graph where edges do not have a specific direction, meaning connections go both ways. If two places are connected, you can travel in either direction. Examples include friendships on social media and two-way roads.

10. Weighted Graphs

A weighted graph is a graph where each edge has a number (weight) that represents distance, cost, or time. These graphs help find the shortest or cheapest paths. Examples include Google Maps, airline routes, and delivery networks.

11. Unweighted Graphs

An unweighted graph is a graph where all edges are treated equally, with no extra values like distance or cost. It simply shows connections between points. Examples include basic social networks and metro maps without travel times.

12. Pseudo Graph

A graph G with a self-loop and some multiple edges is called a pseudo graph. A pseudograph is a type of graph that allows for the existence of self-loops (edges that connect a vertex to itself) and multiple edges (more than one edge connecting two vertices). In contrast, a simple graph is a graph that does not allow for loops or multiple edges. 

13. Regular Graph

A simple graph is said to be regular if all vertices of graph G are of equal degree. All complete graphs are regular but vice versa is not possible. A regular graph is a type of undirected graph where every vertex has the same number of edges or neighbors. In other words, if a graph is regular, then every vertex has the same degree. 

14. Bipatite Graph

A graph in which the vertices can be divided into two disjoint sets such that every edge connects a vertex in one set to a vertex in the other set.

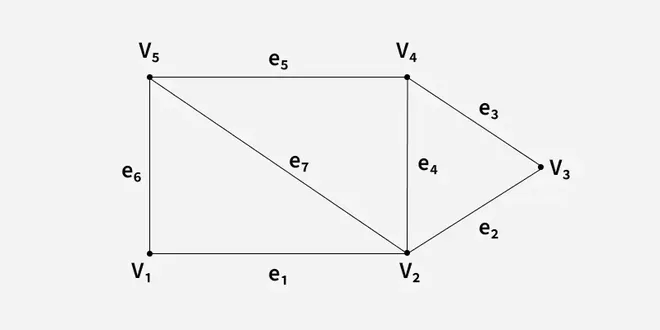
A graph G = (V, E) is said to be a bipartite graph if its vertex set V(G) can be partitioned into two non-empty disjoint subsets. V1(G) and V2(G) in such a way that each edge e of E(G) has one end in V1(G) and another end in V2(G). The partition V1 U V2 = V is called Bipartite of G. Here in the figure: V1(G)={V5, V4, V3} and V2(G)={V1, V2} 

15. Labeled Graph

If the vertices and edges of a graph are labeled with name, date, or weight then it is called a labeled graph. It is also called Weighted Graph. 

16. Sparse Graphs

A graph with relatively few edges compared to the number of vertices. Example: A chemical reaction graph where each vertex represents a chemical compound and each edge represents a reaction between two compounds.

17. Dense Graphs

A graph with many edges compared to the number of vertices. Example: A social network graph where each vertex represents a person and each edge represents a friendship.

18. Digraph Graph

A graph G = (V, E) with a mapping f such that every edge maps onto some ordered pair of vertices (Vi, Vj) are called a Digraph. It is also called Directed Graph. The ordered pair (Vi, Vj) means an edge between Vi and Vj with an arrow directed from Vi to Vj. Here in the figure: e1 = (V1, V2) e2 = (V2, V3) e4 = (V2, V4) 

19. Subgraph

A graph G1 = (V1, E1) is called a subgraph of a graph G(V, E) if V1(G) is a subset of V(G) and E1(G) is a subset of E(G) such that each edge of G1 has same end vertices as in G. 

 20. Connected or Disconnected Graph

Graph G is said to be connected if any pair of vertices (Vi, Vj) of a graph G is reachable from one another. Or a graph is said to be connected if there exists at least one path between each and every pair of vertices in graph G, otherwise, it is disconnected. A null graph with n vertices is a disconnected graph consisting of n components. Each component consists of one vertex and no edge. 

21. Cyclic Graph

A graph G consisting of n vertices and n> = 3 that is V1, V2, V3- – – – Vn and edges (V1, V2), (V2, V3), (V3, V4)- – – – (Vn, V1) are called cyclic graph. 

22. Trees

A connected graph with no cycles. Example: A family tree where each person is connected to their parents.

23. Types of Subgraphs

• Vertex disjoint subgraph: Any two graph G1 = (V1, E1) and G2 = (V2, E2) are said to be vertex disjoint of a graph G = (V, E) if V1(G1) intersection V2(G2) = null. In the figure, there is no common vertex between G1 and G2.
• Edge disjoint subgraph: A subgraph is said to be edge-disjoint if E1(G1) intersection E2(G2) = null. In the figure, there is no common edge between G1 and G2.

Note: Edge disjoint subgraph may have vertices in common but a vertex disjoint graph cannot have a common edge, so the vertex disjoint subgraph will always be an edge-disjoint subgraph.

24. Spanning Subgraph

Consider the graph G(V,E) as shown below. A spanning subgraph is a subgraph that contains all the vertices of the original graph G that is G'(V’,E’) is spanning if V’=V and E’ is a subset of E.

So one of the spanning subgraph can be as shown below G'(V’,E’). It has all the vertices of the original graph G and some of the edges of G.

This is just one of the many spanning subgraphs of graph G. We can create various other spanning subgraphs by different combinations of edges. Note that if we consider a graph G'(V’,E’) where V’=V and E’=E, then graph G’ is a spanning subgraph of graph G(V,E).

Advantages of graphs

1. Graphs can be used to model and analyze complex systems and relationships.
2. They are useful for visualizing and understanding data.
3. Graph algorithms are widely used in computer science and other fields, such as social network analysis, logistics, and transportation.
4. Graphs can be used to represent a wide range of data types, including social networks, road networks, and the internet.

Disadvantages of graphs

1. Large graphs can be difficult to visualize and analyze.
2. Graph algorithms can be computationally expensive, especially for large graphs.
3. The interpretation of graph results can be subjective and may require domain-specific knowledge.
4. Graphs can be susceptible to noise and outliers, which can impact the accuracy of analysis results.

Related article: Applications, Advantages and Disadvantages of Graph