Construct Full Binary Tree from given preorder and postorder traversals

Last Updated : 05 Nov, 2024

Given two arrays that represent preorder and postorder traversals of a full binary tree, construct the binary tree. Full Binary Tree is a binary tree where every node has either 0 or 2 children.

Examples of Full Trees.

Input: pre[] = [1, 2, 4, 8, 9, 5, 3, 6, 7] , post[] = [8, 9, 4, 5, 2, 6, 7, 3, 1]
Output:

Input: pre[] = [1, 2, 4, 5, 3, 6, 7] , post[] = [4, 5, 2, 6, 7, 3, 1]
Output:

It is not possible to construct a general Binary Tree from preorder and postorder traversals (Please refer to If you are given two traversal sequences, can you construct the binary tree?). But if you know that the Binary Tree is Full, we can construct the tree without ambiguity.

Let us consider the two given arrays as pre[] = {1, 2, 4, 8, 9, 5, 3, 6, 7} and post[] = {8, 9, 4, 5, 2, 6, 7, 3, 1};
In pre[], the leftmost element is root of tree. Since the tree is full and array size is more than 1. The value next to 1 in pre[], must be left child of root. So we know 1 is root and 2 is left child. How to find the all nodes in left subtree? We know 2 is root of all nodes in left subtree. All nodes before 2 in post[] must be in left subtree. Now we know 1 is root, elements {8, 9, 4, 5, 2} are in left subtree, and the elements {6, 7, 3} are in right subtree.

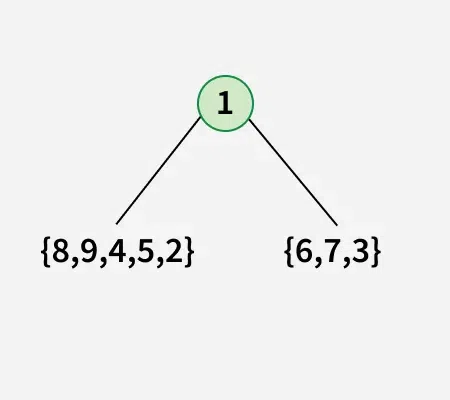
We recursively follow the above approach and get the following tree.

C++

// C++ code for construction of full binary tree 

#include <bits/stdc++.h>
#include <vector>

using namespace std;

class Node {
public:
    int data;
    Node *left;
    Node *right;
    Node(int x) {
        data = x;
        left = right = nullptr;
    }
};

// A recursive function to construct Full from pre[] and post[]. 
// preIndex is used to keep track of index in pre[].
// l is low index and h is high index for the current 
// subarray in post[]
Node* constructTreeUtil (vector<int> &pre, vector<int> &post, int &preIndex,
                          int l, int h, int size) {
  
    if (preIndex >= size || l > h)
        return nullptr;

    // The first node in preorder traversal is root. 
  	// So take the node at preIndex from preorder and make it root,
  	// and increment preIndex
    Node* root = new Node(pre[preIndex]);
    ++preIndex;

    // If the current subarray has only one element, 
  	// no need to recur
    if (l == h)
        return root;

    // Search the next element of pre[] in post[]
    int i;
    for (i = l; i <= h; ++i)
        if (pre[preIndex] == post[i])
            break;

    // Use the index of element found in 
  	// postorder to divide postorder array in two parts:
  	// left subtree and right subtree
    if (i <= h) {
        root->left = constructTreeUtil(pre, post, 
                                       preIndex, l, i, size);
        root->right = constructTreeUtil(pre, post, 
                                        preIndex, i + 1, h - 1, size);
    }

    return root;
}

// The main function to construct Full Binary Tree from given preorder and 
// postorder traversals. This function mainly uses constructTreeUtil()
Node *constructTree (vector<int> &pre, vector<int> &post) {
    int preIndex = 0;
    int size = pre.size();
    return constructTreeUtil(pre, post, preIndex, 
                             0, size - 1, size);
}

// A utility function to print inorder 
// traversal of a Binary Tree
void print (Node* curr) {
    if (curr == nullptr)
        return;
    print(curr->left);
    printf("%d ", curr->data);
    print(curr->right);
}

int main () {
  
    vector<int> pre = {1, 2, 4, 8, 9, 5, 3, 6, 7};
    vector<int> post = {8, 9, 4, 5, 2, 6, 7, 3, 1};

    Node *root = constructTree(pre, post);

    print(root);

    return 0;
}

Java

// Java code for construction of full binary tree
// from given preorder and postorder traversals

import java.util.Arrays;
import java.util.List;

class Node {
    int data;
    Node left, right;

    Node(int x) {
        data = x;
        left = right = null;
    }
}

class GfG {

    // A recursive function to construct Full from pre[] and
    // post[]. preIndex is used to keep track of index in
    // pre[]. l is low index and h is high index for the
    // current subarray in post[]
    static Node constructTreeUtil(List<Integer> pre,
                                  List<Integer> post,
                                  int[] preIndex, int l,
                                  int h, int size) {

        if (preIndex[0] >= size || l > h)
            return null;

        // The first node in preorder traversal is root.
        // So take the node at preIndex from preorder and
        // make it root, and increment preIndex
        Node root = new Node(pre.get(preIndex[0]));
        preIndex[0]++;

        // If the current subarray has only one
        // element, no need to recur
        if (l == h)
            return root;

        // Search the next element of pre[] in post[]
        int i;
        for (i = l; i <= h; ++i)
            if (pre.get(preIndex[0]) == post.get(i))
                break;

        // Use the index of element found in
        // postorder to divide postorder array in two parts:
        // left subtree and right subtree
        if (i <= h) {
            root.left = constructTreeUtil(
                pre, post, preIndex, l, i, size);
            root.right = constructTreeUtil(
                pre, post, preIndex, i + 1, h - 1, size);
        }

        return root;
    }

    // The main function to construct Full Binary Tree from
    // given preorder and postorder traversals. This
    // function mainly uses constructTreeUtil()
    static Node constructTree(List<Integer> pre,
                              List<Integer> post) {
        int[] preIndex = { 0 };
        int size = pre.size();
        return constructTreeUtil(pre, post, preIndex, 0,
                                 size - 1, size);
    }

    // A utility function to print inorder traversal of a
    // Binary Tree
    static void print(Node curr) {
        if (curr == null)
            return;
        print(curr.left);
        System.out.print(curr.data + " ");
        print(curr.right);
    }

    public static void main(String[] args) {
        List<Integer> pre
            = Arrays.asList(1, 2, 4, 8, 9, 5, 3, 6, 7);
        List<Integer> post
            = Arrays.asList(8, 9, 4, 5, 2, 6, 7, 3, 1);

        Node root = constructTree(pre, post);

        print(root);
    }
}

Python

# Python3 program for construction of
# full binary tree

class Node:
    def __init__(self, x):
        self.data = x
        self.left = None
        self.right = None


def construct_tree_util(pre, post, pre_index, l, h):
    if pre_index[0] >= len(pre) or l > h:
        return None

    # The first node in preorder traversal is root
    root = Node(pre[pre_index[0]])
    pre_index[0] += 1

    # If the current subarray has only one element,
    # no need to recur
    if l == h:
        return root

    # Search the next element of pre[] in post[]
    i = 0
    for i in range(l, h + 1):
        if pre[pre_index[0]] == post[i]:
            break

    # Use the index found in postorder to
    # divide into left and right subtrees
    if i <= h:
        root.left = construct_tree_util\
        		(pre, post, pre_index, l, i)
        root.right = construct_tree_util\
        		(pre, post, pre_index, i + 1, h - 1)

    return root


def construct_tree(pre, post):
    pre_index = [0]
    return construct_tree_util\
  		(pre, post, pre_index, 0, len(post) - 1)

def print_inorder(node):
    if node is None:
        return
    print_inorder(node.left)
    print(node.data, end=' ')
    print_inorder(node.right)


if __name__ == "__main__":
    pre = [1, 2, 4, 8, 9, 5, 3, 6, 7]
    post = [8, 9, 4, 5, 2, 6, 7, 3, 1]

    root = construct_tree(pre, post)
    print_inorder(root)
    print()

// C# code for construction of full binary
// tree from given preorder and postorder traversals

using System;
using System.Collections.Generic;

class Node {
    public int data;
    public Node left, right;

    public Node(int x) {
        data = x;
        left = right = null;
    }
}

class GfG {

    // A recursive function to construct Full from pre[] and
    // post[]. preIndex is used to keep track of index in
    // pre[]. l is low index and h is high index for the
    // current subarray in post[]
    static Node ConstructTreeUtil(List<int> pre,
                                  List<int> post,
                                  ref int preIndex, int l,
                                  int h, int size) {

        if (preIndex >= size || l > h)
            return null;

        // The first node in preorder traversal is root. So
        // take the node at preIndex from preorder and make
        // it root, and increment preIndex
        Node root = new Node(pre[preIndex]);
        preIndex++;

        // If the current subarray has only one element, no
        // need to recur
        if (l == h)
            return root;

        // Search the next element of pre[] in post[]
        int i;
        for (i = l; i <= h; ++i)
            if (pre[preIndex] == post[i])
                break;

        // Use the index of element found in postorder to
        // divide postorder array in two parts: left subtree
        // and right subtree
        if (i <= h) {
            root.left = ConstructTreeUtil(
                pre, post, ref preIndex, l, i, size);
            root.right
                = ConstructTreeUtil(pre, post, ref preIndex,
                                    i + 1, h - 1, size);
        }

        return root;
    }

    // The main function to construct Full Binary Tree from
    // given preorder and postorder traversals. This
    // function mainly uses constructTreeUtil()
    static Node ConstructTree(List<int> pre,
                                     List<int> post) {
        int preIndex = 0;
        int size = pre.Count;
        return ConstructTreeUtil(pre, post, ref preIndex, 0,
                                 size - 1, size);
    }

    // A utility function to print inorder traversal of a
    // Binary Tree
    static void Print(Node curr) {
        if (curr == null)
            return;
        Print(curr.left);
        Console.Write(curr.data + " ");
        Print(curr.right);
    }

    static void Main(string[] args) {
        List<int> pre
            = new List<int>{ 1, 2, 4, 8, 9, 5, 3, 6, 7 };
        List<int> post
            = new List<int>{ 8, 9, 4, 5, 2, 6, 7, 3, 1 };

        Node root = ConstructTree(pre, post);

        Print(root);
    }
}

JavaScript

// Javascript code for construction of full binary tree

class Node {
    constructor(data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

function constructTreeUtil(pre, post, preIndex, l, h) {
    if (preIndex[0] >= pre.length || l > h) {
        return null;
    }

    // The first node in preorder traversal is root
    const root = new Node(pre[preIndex[0]]);
    preIndex[0]++;

    // If the current subarray has only one element, no need
    // to recur
    if (l === h) {
        return root;
    }

    // Search the next element of pre[] in post[]
    let i;
    for (i = l; i <= h; i++) {
        if (pre[preIndex[0]] === post[i]) {
            break;
        }
    }

    // Use the index found in postorder to
    // divide into left and right subtrees
    if (i <= h) {
        root.left
            = constructTreeUtil(pre, post, preIndex, l, i);
        root.right = constructTreeUtil(pre, post, preIndex,
                                       i + 1, h - 1);
    }

    return root;
}

function constructTree(pre, post) {
    const preIndex = [ 0 ];
    return constructTreeUtil(pre, post, preIndex, 0,
                             post.length - 1);
}

function printInorder(node) {
    if (node === null) {
        return;
    }
    printInorder(node.left);
    console.log(node.data + " ");
    printInorder(node.right);
}

const pre = [ 1, 2, 4, 8, 9, 5, 3, 6, 7 ];
const post = [ 8, 9, 4, 5, 2, 6, 7, 3, 1 ];

const root = constructTree(pre, post);
printInorder(root);
console.log();