Program to Print Pascal's Triangle

Last Updated : 23 Jul, 2025

Try it on GfG Practice

Given an integer n, the task is to find the first n rows of Pascal's triangle. Pascal's triangle is a triangular array of binomial coefficients.

Examples:

Example1: The below image shows the Pascal's Triangle for n=4

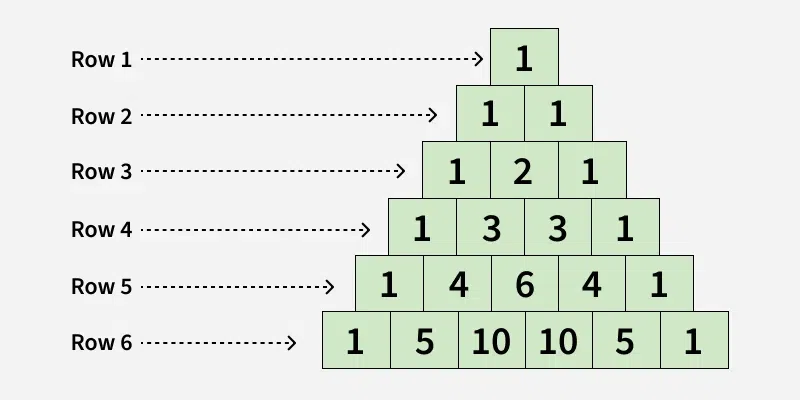
Example2: The below image shows the Pascal's Triangle for n = 6

Table of Content

[Naive Approach] Using Binomial Coefficient
[Better Approach] Using Dynamic Programming
[Expected Approach] Using Binomial Coefficient (Space Optimized)

[Naive Approach] Using Binomial Coefficient

The number of entries in every row is equal to row number (1-based). For example, the first row has "1", the second row has "1 1", the third row has "1 2 1",.. and so on. Every entry in a row is value of a Binomial Coefficient.

Example of Binomial Coefficient:
(a+b)ⁿ= ⁿC₀*aⁿb⁰+ ⁿC₁*a^n-1b¹+ ⁿC₂*a^n-2b² . . . . . . . . + ⁿC_n-1*a¹b^n-1+ ⁿC_n*a⁰bⁿwhere ⁿC_i is binomial coefficient.
Binomial coefficient

The value of ith entry in row number is ⁿC_i . The value can be calculated using following formula.
ⁿC_i = n! / (i! * (n-i)!) - ith element of nth row

Run a loop for each row of pascal's triangle i.e. 1 to n. For each row, loop through its elements and calculate their binomial coefficients as described in the approach.

C++

// Cpp program for Pascal's Triangle using Binomial
// Coefficient in O(n^3) and O(1) Space
#include <iostream>
#include <vector>
using namespace std;

int binomialCoeff(int n, int k) {
    int res = 1;
    if (k > n - k)
        k = n - k;
    for (int i = 0; i < k; ++i) {
        res *= (n - i);
        res /= (i + 1);
    }

    return res;
}

// Function to print first n rows
// of Pascal's Triangle
vector<vector<int>> printPascal(int n) {
    vector<vector<int>> mat;
  
  	// Iterate through every row and
    // print entries in it
    for (int row = 0; row < n; row++) {

        // Every row has number of
        // integers equal to row
        // number
        vector<int> arr;
        for (int i = 0; i <= row; i++)
            arr.push_back(binomialCoeff(row, i));

        mat.push_back(arr);
    }
    return mat;
}

int main() {
  
    int n = 5;
    vector<vector<int>> mat = printPascal(n);
    for (int i = 0; i < mat.size(); i++) {
        for (int j = 0; j < mat[i].size(); j++) {
            cout << mat[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

Java

// Java program for Pascal's Triangle using Binomial
// Coefficient in O(n^3) and O(1) Space 

import java.util.*;

class GfG {

    static int binomialCoeff(int n, int k) {
        int res = 1;
        if (k > n - k)
            k = n - k;
        for (int i = 0; i < k; ++i) {
            res *= (n - i);
            res /= (i + 1);
        }
        return res;
    }

    // Function to print first n rows 
    // of Pascal's Triangle 
    static List<List<Integer>> printPascal(int n) {
        List<List<Integer>> mat = new ArrayList<>();
      
        // Iterate through every row and
    	// print entries in it
        for (int row = 0; row < n; row++) {
            List<Integer> arr = new ArrayList<>();
            for (int i = 0; i <= row; i++)
                arr.add(binomialCoeff(row, i));
            mat.add(arr);
        }
        return mat;
    }

    public static void main(String[] args) {
        int n = 5;
        List<List<Integer>> mat = printPascal(n);
        for (int i = 0; i < mat.size(); i++) {
            for(int j = 0; j < mat.get(i).size(); j++) {
                System.out.print(mat.get(i).get(j) + " ");
            }
            System.out.println();
        }
    }
}

Python

# Python program for Pascal's Triangle using Binomial
# Coefficient in O(n^3) and O(1) Space 

def binomialCoeff(n, k):
    res = 1
    if k > n - k:
        k = n - k
    for i in range(k):
        res *= (n - i)
        res //= (i + 1)
    return res

# Function to print first n rows 
# of Pascal's Triangle 
def printPascal(n):
    mat = []
    
    # Iterate through every row and
    # print entries in it
    for row in range(n):
        arr = []
        for i in range(row + 1):
            arr.append(binomialCoeff(row, i))
        mat.append(arr)
    return mat

n = 5
mat = printPascal(n)
for i in range(len(mat)):
    for j in range(len(mat[i])):
        print(mat[i][j], end=" ")
    print()

C#

// C# program for Pascal's Triangle using Binomial
// Coefficient in O(n^3) and O(1) Space 

using System;
using System.Collections.Generic;

class GfG {
    static int binomialCoeff(int n, int k) {
        int res = 1;
        if (k > n - k)
            k = n - k;
        for (int i = 0; i < k; ++i)
        {
            res *= (n - i);
            res /= (i + 1);
        }
        return res;
    }

    // Function to print first n rows 
    // of Pascal's Triangle 
    static List<List<int>> printPascal(int n) {
        List<List<int>> mat = new List<List<int>>();
      
      	// Iterate through every row and
    	// print entries in it
        for (int row = 0; row < n; row++) {
            List<int> arr = new List<int>();
            for (int i = 0; i <= row; i++)
                arr.Add(binomialCoeff(row, i));
            mat.Add(arr);
        }
        return mat;
    }

    static void Main() {
        int n = 5;
        List<List<int>> mat = printPascal(n);
        for (int i = 0; i < mat.Count; i++) {
            for(int j = 0; j < mat[i].Count; j++) {
                Console.Write(mat[i][j] + " ");
            }
            Console.WriteLine();
        }
    }
}

JavaScript

// JavaScript program for Pascal's Triangle using Binomial
// Coefficient in O(n^3) and O(1) Space 

function binomialCoeff(n, k) {
    let res = 1;
    if (k > n - k)
        k = n - k;
    for (let i = 0; i < k; ++i) {
        res *= (n - i);
        res /= (i + 1);
    }
    return res;
}

// Function to print first n rows 
// of Pascal's Triangle 
function printPascal(n) {
    const mat = [];
    
    // Iterate through every row and
    // print entries in it
    for (let row = 0; row < n; row++) {
        const arr = [];
        for (let i = 0; i <= row; i++)
            arr.push(binomialCoeff(row, i));
        mat.push(arr);
    }
    return mat;
}

const n = 5;
const mat = printPascal(n);
for (let i = 0; i < mat.length; i++) {
    let line = "";
    for(let j = 0; j < mat[i].length; j++) {
        line += mat[i][j] + " ";
    }
    console.log(line);
}

Output

Time Complexity - O(n³)
Auxiliary Space - O(1)

[Better Approach] Using Dynamic Programming

If we take a closer at the triangle, we observe that every entry is sum of the two values above it. So using dynamic programming we can create a 2D array that stores previously generated values. In order to generate a value in a line, we can use the previously stored values from array.
Pascal 's Triangle

Cases:
If row == 0 or row == i
arr[row][i] =1
Else:
arr[row][i] = arr[row-1][i-1] + arr[row-1][i]

C++

// Cpp program for Pascal’s Triangle Using Dynamic 
// Programming in O(n^2) time and O(n^2) extra space 

#include <bits/stdc++.h>
using namespace std;

vector<vector<int>> printPascal(int n) {
    
    // An auxiliary array to store 
    // generated pascal triangle values
    vector<vector<int>> mat;

    // Iterate through every line and 
    // print integer(s) in it
    for (int row = 0; row < n; row++) {
      
        // Every line has number of integers 
        // equal to line number
      	vector<int>arr;
        for (int i = 0; i <= row; i++) {
          
        // First and last values in every row are 1
        if (row == i || i == 0)
            arr.push_back(1);
          
        // Other values are sum of values just 
        // above and left of above
        else
            arr.push_back(mat[row - 1][i - 1] + 
                            mat[row - 1][i]);
        }
        mat.push_back(arr);
    }
  return mat;
}

int main() {
    int n = 5;
    vector<vector<int>> mat = printPascal(n);
    for (int i = 0; i < mat.size(); i++) {
        for (int j = 0; j < mat[i].size(); j++) {
            	cout << mat[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

C

#include <stdio.h>
#include <stdlib.h>

int** printPascal(int n) {
    // An auxiliary array to store 
    // generated pascal triangle values
    int** mat = (int**)malloc(n * sizeof(int*));
    for (int i = 0; i < n; i++) {
        mat[i] = (int*)malloc((i + 1) * sizeof(int));
    }

    // Iterate through every line and 
    // print integer(s) in it
    for (int row = 0; row < n; row++) {
        // Every line has number of integers 
        // equal to line number
        for (int i = 0; i <= row; i++) {
            // First and last values in every row are 1
            if (row == i || i == 0)
                mat[row][i] = 1;
            // Other values are sum of values just 
            // above and left of above
            else
                mat[row][i] = mat[row - 1][i - 1] + mat[row - 1][i];
        }
    }
    return mat;
}

int main() {
    int n = 5;
    int** mat = printPascal(n);
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= i; j++) {
            printf("%d ", mat[i][j]);
        }
        printf("\n");
    }
    return 0;
}

Java

// Java program for Pascal’s Triangle Using Dynamic 
// Programming in O(n^2) time and O(n^2) extra space 

import java.util.*;

class GfG {

    static List<List<Integer>> printPascal(int n) {
        
        // An auxiliary array to store 
        // generated pascal triangle values
        List<List<Integer>> mat = new ArrayList<>();

        // Iterate through every line and 
        // print integer(s) in it
        for (int row = 0; row < n; row++) {
          
            // Every line has number of integers 
            // equal to line number
            List<Integer> arr = new ArrayList<>();
            for (int i = 0; i <= row; i++) {
              
                // First and last values in every row are 1
                if (row == i || i == 0)
                    arr.add(1);
                  
                // Other values are sum of values just 
                // above and left of above
                else
                    arr.add(mat.get(row - 1).get(i - 1) + 
                            mat.get(row - 1).get(i));
            }
            mat.add(arr);
        }
        return mat;
    }

    public static void main(String[] args) {
        int n = 5;
        List<List<Integer>> mat = printPascal(n);
        for (int i = 0; i < mat.size(); i++) {
            for(int j = 0; j < mat.get(i).size(); j++) {
                    System.out.print(mat.get(i).get(j) + " ");
            }
            System.out.println();
        }
    }
}

Python

# Python program for Pascal’s Triangle Using Dynamic 
# Programming in O(n^2) time and O(n^2) extra space 

def printPascal(n):
    
    # An auxiliary array to store 
    # generated pascal triangle values
    mat = []

    # Iterate through every line and 
    # print integer(s) in it
    for row in range(n):
      
        # Every line has number of integers 
        # equal to line number
        arr = []
        for i in range(row + 1):
          
            # First and last values in every row are 1
            if row == i or i == 0:
                arr.append(1)
              
            # Other values are sum of values just 
            # above and left of above
            else:
                arr.append(mat[row - 1][i - 1] + mat[row - 1][i])
        mat.append(arr)
    return mat

n = 5
mat = printPascal(n)
for i in range(len(mat)):
    for j in range(len(mat[i])):
        print(mat[i][j], end=" ")
    print()

C#

// C# program for Pascal’s Triangle Using Dynamic 
// Programming in O(n^2) time and O(n^2) extra space 

using System;
using System.Collections.Generic;

class GfG {
    static List<List<int>> printPascal(int n) {
        
        // An auxiliary array to store 
        // generated pascal triangle values
        List<List<int>> mat = new List<List<int>>();

        // Iterate through every line and 
        // print integer(s) in it
        for (int row = 0; row < n; row++) {
          
            // Every line has number of integers 
            // equal to line number
            List<int> arr = new List<int>();
            for (int i = 0; i <= row; i++) {
              
                // First and last values in every row are 1
                if (row == i || i == 0)
                    arr.Add(1);
                  
                // Other values are sum of values just 
                // above and left of above
                else
                    arr.Add(mat[row - 1][i - 1] + mat[row - 1][i]);
            }
            mat.Add(arr);
        }
        return mat;
    }

    static void Main() {
        int n = 5;
        List<List<int>> mat = printPascal(n);
        for (int i = 0; i < mat.Count; i++) {
            for(int j = 0; j < mat[i].Count; j++) {
                        Console.Write(mat[i][j] + " ");
            }
            Console.WriteLine();
        }
    }
}

JavaScript

// JavaScript program for Pascal’s Triangle Using Dynamic 
// Programming in O(n^2) time and O(n^2) extra space 

function printPascal(n) {
    
    // An auxiliary array to store 
    // generated pascal triangle values
    const mat = [];

    // Iterate through every line and 
    // print integer(s) in it
    for (let row = 0; row < n; row++) {
      
        // Every line has number of integers 
        // equal to line number
        const arr = [];
        for (let i = 0; i <= row; i++) {
          
            // First and last values in every row are 1
            if (row === i || i === 0)
                arr.push(1);
              
            // Other values are sum of values just 
            // above and left of above
            else
                arr.push(mat[row - 1][i - 1] + mat[row - 1][i]);
        }
        mat.push(arr);
    }
    return mat;
}

const n = 5;
const mat = printPascal(n);
for (let i = 0; i < mat.length; i++) {
    let line = "";
    for(let j = 0; j < mat[i].length; j++) {
            line += mat[i][j] + " ";
    }
    console.log(line);
}

Output

Time Complexity - O(n²)
Auxiliary Space - O(n²)

Note: This method can be optimized to use O(n) extra space as we need values only from previous row. So we can create an auxiliary array of size n and overwrite values. Following is another method uses only O(1) extra space.

[Expected Approach] Using Binomial Coefficient (Space Optimized)

This method is based on approach using Binomial Coefficient. We know that ith entry in a row (n) in Binomial Coefficient is ⁿC_i and all rows start with value 1. The idea is to calculate ⁿC_i-1 using ⁿC_i. It can be calculated in O(1) time.
ⁿC_i = n! / (i! * (n-i)!) - (Eq - 1)
ⁿC_i-1 = n! / ((i-1)! * (n-i+1)!) - (Eq - 2)
On solving Eq- 1 further , we get ⁿC_i = n! / (n-i)! * i * (i-1)!) - (Eq - 3)
On solving Eq- 2 further , we get ⁿC_i-1 = n! / ((n- i + 1) * (n-i)! * (i-1)! ) - (Eq - 4)
Now, divide Eq - 3 by Eq - 4:
ⁿC_i= ⁿC_i-1* (n-i+1) / i , So ⁿC_i can be calculated from ⁿC_i-1in O(1) time

C++

// C++ program for Pascal’s Triangle
// in O(n^2) time and O(1) extra space
#include <bits/stdc++.h>
using namespace std;

// function for Pascal's Triangle
void printPascal(int n) {
    for (int row = 1; row <= n; row++) {
      
      	// nC0 = 1
        int c = 1; 
        for (int i = 1; i <= row; i++) {

            // The first value in a row is always 1
          	cout << c << " ";
            c = c * (row - i) / i;
        }
        cout << endl;
    }
}

int main() {
    int n = 5;
    printPascal(n);
    return 0;
}

C

// C program for Pascal’s Triangle
#include <stdio.h>

// function for Pascal's Triangle
void printPascal(int n) {
    for (int row = 1; row <= n; row++) {
        // nC0 = 1
        int c = 1; 
        for (int i = 1; i <= row; i++) {
            // The first value in a row is always 1
            printf("%d ", c);
            c = c * (row - i) / i;
        }
        printf("\n");
    }
}

int main() {
    int n = 5;
    printPascal(n);
    return 0;
}

Java

// Java program for Pascal’s Triangle
// in O(n^2) time and O(1) extra space

import java.util.*;

class GfG {

    // function for Pascal's Triangle
    static void printPascal(int n) {
        for (int row = 1; row <= n; row++) {
          
            // nC0 = 1
            int c = 1; 
            for (int i = 1; i <= row; i++) {

                // The first value in a row is always 1
                System.out.print(c + " ");
                c = c * (row - i) / i;
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int n = 5;
        printPascal(n);
    }
}

Python

# Python program for Pascal’s Triangle
# in O(n^2) time and O(1) extra space

# function for Pascal's Triangle
def printPascal(n):
    for row in range(1, n + 1):
      
        # nC0 = 1
        c = 1
        for i in range(1, row + 1):

            # The first value in a row is always 1
            print(c, end=" ")
            c = c * (row - i) // i
        print()

n = 5
printPascal(n)

C#

// C# program for Pascal’s Triangle
// in O(n^2) time and O(1) extra space

using System;
using System.Collections.Generic;

class GfG {
  
    // function for Pascal's Triangle
    static void printPascal(int n) {
        for (int row = 1; row <= n; row++) {
          
            // nC0 = 1
            int c = 1; 
            for (int i = 1; i <= row; i++) {

                // The first value in a row
              	// is always 1
                Console.Write(c + " ");
                c = c * (row - i) / i;
            }
            Console.WriteLine();
        }
    }

    static void Main() {
        int n = 5;
        printPascal(n);
    }
}

JavaScript

// JavaScript program for Pascal’s Triangle
// in O(n^2) time and O(1) extra space

function printPascal(n) {
    for (let row = 1; row <= n; row++) {
      
        // nC0 = 1
        let c = 1;
        let line = "";
        for (let i = 1; i <= row; i++) {

            // The first value in a row is always 1
            line += c + " ";
            c = Math.floor(c * (row - i) / i);
        }
        console.log(line);
    }
}

const n = 5;
printPascal(n);

Output

Time Complexity - O(n²)
Auxiliary Space - O(1)

Related articles:

Find just the one element of a pascal's triangle given row number and column number in O(n) time.
Find a particular row of pascal's triangle given a row number in O(n) time is Find the Nth row in Pascal’s Triangle.

Pascal Triangle | DSA Problem

K

Improve

Article Tags :

Explore