CSES Solutions - Two Knights

Given a number N, the task is to count for each K = 1,2 … N the number of ways two knights can be placed on a K X K chessboard so that they do not attack each other.

Examples:

Input: N = 2
Output: 0 6
Explanation:

• For a 1 X 1 chessboard, there is no possible way to place 2 knights on a 1 X 1 chessboard, ways = 0.
• For a 2 X 2 chessboard, there are 6 ways to place 2 knights on a 2 X 2 chessboard, ways = 6.

Input: N = 8
Output:0 6 28 96 252 550 1056 1848
Explanation:

• For a 1 X 1 chessboard, there is no possible way to place 2 knights on a 1 X 1 chessboard, ways = 0.
• For a 2 X 2 chessboard, there are 6 ways to place 2 knights on a 2 X 2 chessboard, ways = 6.
• For a 3 X 3 chessboard, there are 28 ways to place 2 knights on a 3 X 3 chessboard, ways = 28.
• For a 4 X 4 chessboard, there are 96 ways to place 2 knights on a 4 X 4 chessboard, ways = 96.
• For a 5 X 5 chessboard, there are 252 ways to place 2 knights on a 5 X 5 chessboard, ways = 252.
• For a 6 X 6 chessboard, there are 550 ways to place 2 knights on a 6 X 6 chessboard, ways = 550.
• For a 7 X 7 chessboard, there are 1056 ways to place 2 knights on a 7 X 7 chessboard, ways = 1056.
• For an 8 X 8 chessboard, there are 1848 ways to place 2 knights on an 8 X 8 chessboard, ways = 1848.

Approach: To solve the problem, follow the below idea:

Let's solve this problem for a particular K X K chessboard. Total number of squares in K X K chessboard is K². So, number of ways the first knight can be placed is K². Now the number of ways the second knight can be placed will be K² - 1. This leads us to, the total number of ways the two knights can be placed in K X K chessboard is K² * (K²-1)/2, we divide by 2 because both knights are identical. Now we need to subtract number of ways the two knights attack each other from above equation.

For this we need to observe that the two knights attack each other when they are in a 2 X 3 or 3 X 2 block. The number of ways two knights can attack each other in a 2 X 3 block is 2 and number of ways two knights can attack each other in a 3 X 2 block is 2. Refer to the below figure for better understanding:

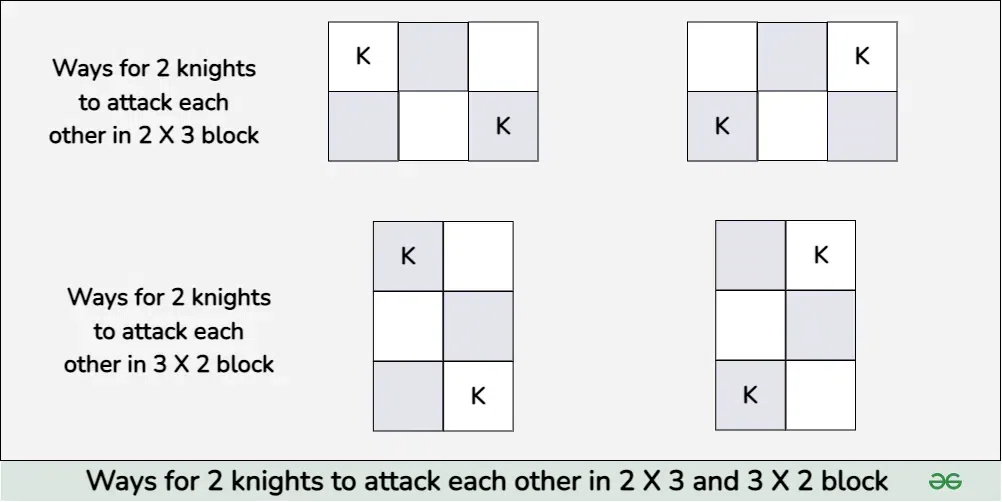
Now, we just need to find the total number of 2 X 3 and 3 X 2 blocks in a K X K chessboard. In a K X K chessboard, the 2*3 blocks can be arranged in (K-1) rows (starting from the first row till the (K-1)-th row), and there are (K-2) ways to position them in columns (starting from the first column till the (K-2)-th column) which gives us (K-1)*(K-2) ways to place a 2 X 3 block in a K X K chessboard. Similarly, we can place a 3 X 2 block in (K - 1) * (K - 2) ways.

So, the total number of ways two knights can attack each other in a K X K chessboard will be sum of 2 * number of 2 X 3 blocks and 2 * number of 3 X 2 blocks, which is 4 * (K - 1) * (K - 2). It is every important to note that no 2 ways of attacking are same in the derived formula.

Hence the total number of ways Two Knights can be placed in a K X K chessboard such that they don't attack each other is:

(K² * (K² - 1)) / 2 - (4 * (K - 1) * (K - 2))

Below is the implementation of above approach:

#include <iostream>
using namespace std;

// Function to calculate and print the number of ways two
// knights can be placed on a K X K chessboard such that
// they do not attack each other
long calculateWays(int K) {
    // Total number of ways two knights can be placed on
    // the chessboard
    long totalWays = ((long) K * K * (K * K - 1)) / 2;

    // Number of ways two knights can attack each other
    long attackingWays = 4 * (K - 1) * (K - 2);

    // Number of ways two knights can be placed without
    // attacking each other
    long ans = totalWays - attackingWays;

    // Return the result for the current chessboard size K
    return ans;
}

// Driver Code
int main() {
    // Input the value of N (size of the chessboard)
    int N = 8;

    // Iterate for all the K sized chessboard
    for (int K = 1; K <= N; K++) {
        cout << calculateWays(K) << " ";
    }

    return 0;
}

public class TwoKnights {

    // Function to calculate and print the number of ways two
    // knights can be placed on a K X K chessboard such that
    // they do not attack each other
    static long calculateWays(int K) {
        // Total number of ways two knights can be placed on
        // the chessboard
        long totalWays = ((long) K * K * (K * K - 1)) / 2;

        // Number of ways two knights can attack each other
        long attackingWays = 4 * (K - 1) * (K - 2);

        // Number of ways two knights can be placed without
        // attacking each other
        long ans = totalWays - attackingWays;

        // Return the result for the current chessboard size K
        return ans;
    }

    // Driver Code
    public static void main(String[] args) {
        // Input the value of N (size of the chessboard)
        int N = 8;

        // Iterate for all the K sized chessboard
        for (int K = 1; K <= N; K++) {
            System.out.print(calculateWays(K) + " ");
        }
    }
}


// This code is contributed by shivamgupta310570

# Function to calculate and print the number of ways two
# knights can be placed on a K X K chessboard such that
# they do not attack each other
def two_knights(K):
    # Total number of ways two knights can be placed on
    # the chessboard
    total_ways = ((K * K) * ((K * K) - 1)) // 2

    # Number of ways two knights can attack each other
    attacking_ways = 4 * (K - 1) * (K - 2)

    # Number of ways two knights can be placed without
    # attacking each other
    ans = total_ways - attacking_ways

    # Return the result for the current chessboard size
    return ans

# Driver Code
def main():
    # Input the value of N (size of the chessboard)
    N = 8

    # Iterate for all the K sized chessboard
    for K in range(1, N + 1):
        print(two_knights(K), end=" ")

if __name__ == "__main__":
    main()

// Function to calculate and print the number of ways two
// knights can be placed on a K X K chessboard such that
// they do not attack each other
function twoKnights(K) {
    // Total number of ways two knights can be placed on
    // the chessboard
    let totalWays = (K * K * (K * K - 1)) / 2;

    // Number of ways two knights can attack each other
    let attackingWays = 4 * (K - 1) * (K - 2);

    // Number of ways two knights can be placed without
    // attacking each other
    let ans = totalWays - attackingWays;

    // Return the result for the current chessboard size
    // K
    return ans;
}

// Driver Code
function main() {
    // Input the value of N (size of the chessboard)
    let N = 8;
    let result = "";

    // Iterate for all the K sized chessboard
    for (let K = 1; K <= N; K++) {
        result += twoKnights(K) + " ";
    }

    // Print the result in a single line
    console.log(result.trim());
}

main();

// This code is Contributed by Ayush Mishra

0 6 28 96 252 550 1056 1848 

Time Complexity: O(N), where N is the number of rows or columns of chessboard.
Auxiliary Space:O(1)