Count pairs from two BSTs whose sum is equal to a given value x
Last Updated :
21 Oct, 2024
Given two BSTs containing n1 and n2 distinct nodes respectively. Given a value x. The task is to count all pairs from both the BSTs whose sum is equal to x.
Examples:
Input :
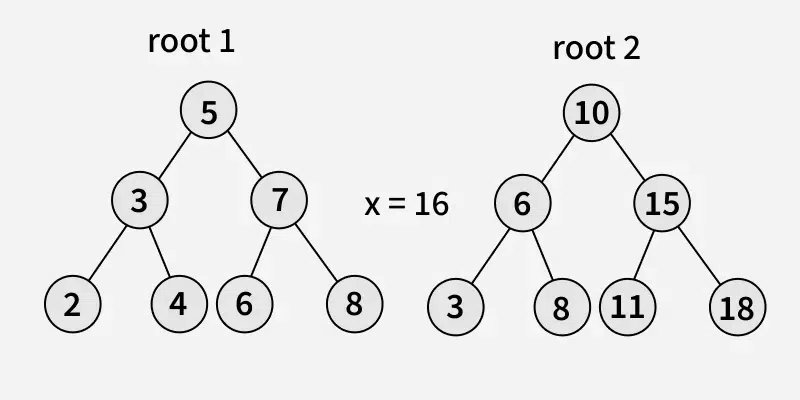
Output: 3
Explanation: The pairs are: (5, 11), (6, 10) and (8, 8) whose sum is equal to x.
[Naive Approach] Using Recursive Method - O(n1 * n2) Time and O(h1 + h2) Space
The idea is traverse the first BST. For each node, find the value of (x-node) in the second BST. If the value exists, then increment the count.
Below is the implementation of the above approach:
C++
// C++ program to find the pairs with
// sum equal to x.
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left, *right;
Node (int x) {
data = x;
left = nullptr;
right = nullptr;
}
};
bool findVal(Node* root, int x) {
if (root == nullptr) return false;
if (root->data == x) return true;
else if (root->data < x)
return findVal(root->right, x);
else
return findVal(root->left, x);
}
// Function to count pairs with sum equal to x
int countPairs(Node* root1, Node* root2, int x) {
// base case
if (root1 == nullptr) return 0;
int ans = 0;
// If pair (root1.data, x-root1.data) exists,
// then increment the ans.
if (findVal(root2, x-root1->data))
ans++;
// Recursively check for left and right subtree.
ans += countPairs(root1->left, root2, x);
ans += countPairs(root1->right, root2, x);
return ans;
}
int main() {
// BST1
// 2
// / \
// 1 3
Node* root1 = new Node(2);
root1->left = new Node(1);
root1->right = new Node(3);
// BST2
// 5
// / \
// 4 6
Node* root2 = new Node(5);
root2->left = new Node(4);
root2->right = new Node(6);
int x = 6;
cout << countPairs(root1, root2, x);
return 0;
}
// Java program to find the pairs with
// sum equal to x.
class Node {
int data;
Node left, right;
Node(int x) {
data = x;
left = null;
right = null;
}
}
class GfG {
static boolean findVal(Node root, int x) {
if (root == null) return false;
if (root.data == x) return true;
else if (root.data < x)
return findVal(root.right, x);
else
return findVal(root.left, x);
}
// Function to count pairs with sum equal to x
static int countPairs(Node root1, Node root2, int x) {
// base case
if (root1 == null) return 0;
int ans = 0;
// If pair (root1.data, x-root1.data) exists,
// then increment the ans.
if (findVal(root2, x - root1.data))
ans++;
// Recursively check for left and right subtree.
ans += countPairs(root1.left, root2, x);
ans += countPairs(root1.right, root2, x);
return ans;
}
public static void main(String[] args) {
// BST1
// 2
// / \
// 1 3
Node root1 = new Node(2);
root1.left = new Node(1);
root1.right = new Node(3);
// BST2
// 5
// / \
// 4 6
Node root2 = new Node(5);
root2.left = new Node(4);
root2.right = new Node(6);
int x = 6;
System.out.println(countPairs(root1, root2, x));
}
}
# Python program to find the pairs with
# sum equal to x.
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
def findVal(root, x):
if root is None:
return False
if root.data == x:
return True
elif root.data < x:
return findVal(root.right, x)
else:
return findVal(root.left, x)
# Function to count pairs with sum equal to x
def countPairs(root1, root2, x):
# base case
if root1 is None:
return 0
ans = 0
# If pair (root1.data, x-root1.data) exists,
# then increment the ans.
if findVal(root2, x - root1.data):
ans += 1
# Recursively check for left and right subtree.
ans += countPairs(root1.left, root2, x)
ans += countPairs(root1.right, root2, x)
return ans
if __name__ == "__main__":
# BST1
# 2
# / \
# 1 3
root1 = Node(2)
root1.left = Node(1)
root1.right = Node(3)
# BST2
# 5
# / \
# 4 6
root2 = Node(5)
root2.left = Node(4)
root2.right = Node(6)
x = 6
print(countPairs(root1, root2, x))
// C# program to find the pairs with
// sum equal to x.
using System;
class Node {
public int data;
public Node left, right;
public Node(int x) {
data = x;
left = null;
right = null;
}
}
class GfG {
static bool findVal(Node root, int x) {
if (root == null) return false;
if (root.data == x) return true;
else if (root.data < x)
return findVal(root.right, x);
else
return findVal(root.left, x);
}
// Function to count pairs with sum equal to x
static int countPairs(Node root1, Node root2, int x) {
// base case
if (root1 == null) return 0;
int ans = 0;
// If pair (root1.data, x-root1.data) exists,
// then increment the ans.
if (findVal(root2, x - root1.data))
ans++;
// Recursively check for left and
// right subtree.
ans += countPairs(root1.left, root2, x);
ans += countPairs(root1.right, root2, x);
return ans;
}
static void Main(string[] args) {
// BST1
// 2
// / \
// 1 3
Node root1 = new Node(2);
root1.left = new Node(1);
root1.right = new Node(3);
// BST2
// 5
// / \
// 4 6
Node root2 = new Node(5);
root2.left = new Node(4);
root2.right = new Node(6);
int x = 6;
Console.WriteLine(countPairs(root1, root2, x));
}
}
// JavaScript program to find the pairs with
// sum equal to x.
class Node {
constructor(x) {
this.data = x;
this.left = null;
this.right = null;
}
}
function findVal(root, x) {
if (root === null) return false;
if (root.data === x) return true;
else if (root.data < x)
return findVal(root.right, x);
else
return findVal(root.left, x);
}
// Function to count pairs with
// sum equal to x
function countPairs(root1, root2, x) {
// base case
if (root1 === null) return 0;
let ans = 0;
// If pair (root1.data, x-root1.data) exists,
// then increment the ans.
if (findVal(root2, x - root1.data))
ans++;
// Recursively check for left and right subtree.
ans += countPairs(root1.left, root2, x);
ans += countPairs(root1.right, root2, x);
return ans;
}
// BST1
// 2
// / \
// 1 3
let root1 = new Node(2);
root1.left = new Node(1);
root1.right = new Node(3);
// BST2
// 5
// / \
// 4 6
let root2 = new Node(5);
root2.left = new Node(4);
root2.right = new Node(6);
let x = 6;
console.log(countPairs(root1, root2, x));
[Expected Approach] Using Iterative method - O(n1 + n2) Time and O(h1 + h2) Space
The idea is to traverse the first BST from smallest to largest value iterative inorder traversal and traverse the second BST from largest to smallest value (reverse in-order). If the sum of nodes is equal to x, them increment the pair count and move both nodes to the next nodes. If the value is less than x, then move the node of first BST. Otherwise, move the node of second BST to the next node.
Below is the implementation of the above approach:
C++
// C++ program to find the pairs with
// sum equal to x.
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left, *right;
Node (int x) {
data = x;
left = nullptr;
right = nullptr;
}
};
// Function to count pairs with sum equal to x
int countPairs(Node* root1, Node* root2, int x) {
// if either of the tree is empty
if (root1 == nullptr || root2 == nullptr)
return 0;
// stack 'st1' used for the inorder
// traversal of BST 1
// stack 'st2' used for the reverse
// inorder traversal of BST 2
stack<Node*> st1, st2;
Node* top1, *top2;
int count = 0;
// the loop will break when either of two
// traversals gets completed
while (1) {
// to find next node in inorder
// traversal of BST 1
while (root1 != nullptr) {
st1.push(root1);
root1 = root1->left;
}
// to find next node in reverse
// inorder traversal of BST 2
while (root2 != nullptr) {
st2.push(root2);
root2 = root2->right;
}
// if either gets empty then corresponding
// tree traversal is completed
if (st1.empty() || st2.empty())
break;
top1 = st1.top();
top2 = st2.top();
// if the sum of the node's is equal to 'x'
if ((top1->data + top2->data) == x) {
count++;
// pop nodes from the respective stacks
st1.pop();
st2.pop();
// insert next possible node in the
// respective stacks
root1 = top1->right;
root2 = top2->left;
}
// move to next possible node in the
// inorder traversal of BST 1
else if ((top1->data + top2->data) < x) {
st1.pop();
root1 = top1->right;
}
// move to next possible node in the
// reverse inorder traversal of BST 2
else {
st2.pop();
root2 = top2->left;
}
}
return count;
}
int main() {
// BST1
// 2
// / \
// 1 3
Node* root1 = new Node(2);
root1->left = new Node(1);
root1->right = new Node(3);
// BST2
// 5
// / \
// 4 6
Node* root2 = new Node(5);
root2->left = new Node(4);
root2->right = new Node(6);
int x = 6;
cout << countPairs(root1, root2, x);
return 0;
}
// Java program to find the pairs with
// sum equal to x.
import java.util.Stack;
class Node {
int data;
Node left, right;
Node(int x) {
data = x;
left = null;
right = null;
}
}
class GfG {
// Function to count pairs with sum equal to x
static int countPairs(Node root1, Node root2, int x) {
// if either of the tree is empty
if (root1 == null || root2 == null)
return 0;
// stack 'st1' used for the inorder
// traversal of BST 1
// stack 'st2' used for the reverse
// inorder traversal of BST 2
Stack<Node> st1 = new Stack<>();
Stack<Node> st2 = new Stack<>();
Node top1, top2;
int count = 0;
// the loop will break when either of two
// traversals gets completed
while (true) {
// to find next node in inorder
// traversal of BST 1
while (root1 != null) {
st1.push(root1);
root1 = root1.left;
}
// to find next node in reverse
// inorder traversal of BST 2
while (root2 != null) {
st2.push(root2);
root2 = root2.right;
}
// if either gets empty then corresponding
// tree traversal is completed
if (st1.isEmpty() || st2.isEmpty())
break;
top1 = st1.peek();
top2 = st2.peek();
// if the sum of the node's is equal to 'x'
if ((top1.data + top2.data) == x) {
count++;
// pop nodes from the respective stacks
st1.pop();
st2.pop();
// insert next possible node in the
// respective stacks
root1 = top1.right;
root2 = top2.left;
}
// move to next possible node in the
// inorder traversal of BST 1
else if ((top1.data + top2.data) < x) {
st1.pop();
root1 = top1.right;
}
// move to next possible node in the
// reverse inorder traversal of BST 2
else {
st2.pop();
root2 = top2.left;
}
}
return count;
}
public static void main(String[] args) {
// BST1
// 2
// / \
// 1 3
Node root1 = new Node(2);
root1.left = new Node(1);
root1.right = new Node(3);
// BST2
// 5
// / \
// 4 6
Node root2 = new Node(5);
root2.left = new Node(4);
root2.right = new Node(6);
int x = 6;
System.out.println(countPairs(root1, root2, x));
}
}
# Python program to find the pairs with
# sum equal to x.
class Node:
def __init__(self, x):
self.data = x
self.left = None
self.right = None
# Function to count pairs with sum equal to x
def countPairs(root1, root2, x):
# if either of the tree is empty
if root1 is None or root2 is None:
return 0
# stack 'st1' used for the inorder
# traversal of BST 1
# stack 'st2' used for the reverse
# inorder traversal of BST 2
st1, st2 = [], []
count = 0
# the loop will break when either of two
# traversals gets completed
while True:
# to find next node in inorder
# traversal of BST 1
while root1 is not None:
st1.append(root1)
root1 = root1.left
# to find next node in reverse
# inorder traversal of BST 2
while root2 is not None:
st2.append(root2)
root2 = root2.right
# if either gets empty then corresponding
# tree traversal is completed
if not st1 or not st2:
break
top1 = st1[-1]
top2 = st2[-1]
# if the sum of the node's is equal to 'x'
if (top1.data + top2.data) == x:
count += 1
# pop nodes from the
# respective stacks
st1.pop()
st2.pop()
# insert next possible node in the
# respective stacks
root1 = top1.right
root2 = top2.left
# move to next possible node in the
# inorder traversal of BST 1
elif (top1.data + top2.data) < x:
st1.pop()
root1 = top1.right
# move to next possible node in the
# reverse inorder traversal of BST 2
else:
st2.pop()
root2 = top2.left
return count
if __name__ == "__main__":
# BST1
# 2
# / \
# 1 3
root1 = Node(2)
root1.left = Node(1)
root1.right = Node(3)
# BST2
# 5
# / \
# 4 6
root2 = Node(5)
root2.left = Node(4)
root2.right = Node(6)
x = 6
print(countPairs(root1, root2, x))
// C# program to find the pairs with
// sum equal to x.
using System;
using System.Collections.Generic;
class Node {
public int data;
public Node left, right;
public Node(int x) {
data = x;
left = null;
right = null;
}
}
class GfG {
// Function to count pairs with sum
// equal to x
static int countPairs(Node root1, Node root2, int x) {
// if either of the tree is empty
if (root1 == null || root2 == null)
return 0;
// stack 'st1' used for the inorder
// traversal of BST 1
// stack 'st2' used for the reverse
// inorder traversal of BST 2
Stack<Node> st1 = new Stack<Node>();
Stack<Node> st2 = new Stack<Node>();
Node top1, top2;
int count = 0;
// the loop will break when either of two
// traversals gets completed
while (true) {
// to find next node in inorder
// traversal of BST 1
while (root1 != null) {
st1.Push(root1);
root1 = root1.left;
}
// to find next node in reverse
// inorder traversal of BST 2
while (root2 != null) {
st2.Push(root2);
root2 = root2.right;
}
// if either gets empty then corresponding
// tree traversal is completed
if (st1.Count == 0 || st2.Count == 0)
break;
top1 = st1.Peek();
top2 = st2.Peek();
// if the sum of the node's is
// equal to 'x'
if ((top1.data + top2.data) == x) {
count++;
// pop nodes from the
// respective stacks
st1.Pop();
st2.Pop();
// insert next possible node in the
// respective stacks
root1 = top1.right;
root2 = top2.left;
}
// move to next possible node in the
// inorder traversal of BST 1
else if ((top1.data + top2.data) < x) {
st1.Pop();
root1 = top1.right;
}
// move to next possible node in the
// reverse inorder traversal of BST 2
else {
st2.Pop();
root2 = top2.left;
}
}
return count;
}
static void Main(string[] args) {
// BST1
// 2
// / \
// 1 3
Node root1 = new Node(2);
root1.left = new Node(1);
root1.right = new Node(3);
// BST2
// 5
// / \
// 4 6
Node root2 = new Node(5);
root2.left = new Node(4);
root2.right = new Node(6);
int x = 6;
Console.WriteLine(countPairs(root1, root2, x));
}
}
// JavaScript program to find the pairs with
// sum equal to x.
class Node {
constructor(x) {
this.data = x;
this.left = null;
this.right = null;
}
}
// Function to count pairs with sum equal to x
function countPairs(root1, root2, x) {
// if either of the tree is empty
if (root1 === null || root2 === null)
return 0;
// stack 'st1' used for the inorder
// traversal of BST 1
// stack 'st2' used for the reverse
// inorder traversal of BST 2
let st1 = [], st2 = [];
let top1, top2;
let count = 0;
// the loop will break when either of two
// traversals gets completed
while (true) {
// to find next node in inorder
// traversal of BST 1
while (root1 !== null) {
st1.push(root1);
root1 = root1.left;
}
// to find next node in reverse
// inorder traversal of BST 2
while (root2 !== null) {
st2.push(root2);
root2 = root2.right;
}
// if either gets empty then corresponding
// tree traversal is completed
if (st1.length === 0 || st2.length === 0)
break;
top1 = st1[st1.length - 1];
top2 = st2[st2.length - 1];
// if the sum of the node's is equal to 'x'
if ((top1.data + top2.data) === x) {
count++;
// pop nodes from the respective stacks
st1.pop();
st2.pop();
// insert next possible node in the
// respective stacks
root1 = top1.right;
root2 = top2.left;
}
// move to next possible node in the
// inorder traversal of BST 1
else if ((top1.data + top2.data) < x) {
st1.pop();
root1 = top1.right;
}
// move to next possible node in the
// reverse inorder traversal of BST 2
else {
st2.pop();
root2 = top2.left;
}
}
return count;
}
// BST1
// 2
// / \
// 1 3
let root1 = new Node(2);
root1.left = new Node(1);
root1.right = new Node(3);
// BST2
// 5
// / \
// 4 6
let root2 = new Node(5);
root2.left = new Node(4);
root2.right = new Node(6);
let x = 6;
console.log(countPairs(root1, root2, x));
Similar Reads
Binary Search Tree A Binary Search Tree (BST) is a type of binary tree data structure in which each node contains a unique key and satisfies a specific ordering property:All nodes in the left subtree of a node contain values strictly less than the node’s value. All nodes in the right subtree of a node contain values s
4 min read
Introduction to Binary Search Tree Binary Search Tree is a data structure used in computer science for organizing and storing data in a sorted manner. Binary search tree follows all properties of binary tree and for every nodes, its left subtree contains values less than the node and the right subtree contains values greater than the
3 min read
Applications of BST Binary Search Tree (BST) is a data structure that is commonly used to implement efficient searching, insertion, and deletion operations along with maintaining sorted sequence of data. Please remember the following properties of BSTs before moving forward.The left subtree of a node contains only node
3 min read
Applications, Advantages and Disadvantages of Binary Search Tree A Binary Search Tree (BST) is a data structure used to storing data in a sorted manner. Each node in a Binary Search Tree has at most two children, a left child and a right child, with the left child containing values less than the parent node and the right child containing values greater than the p
2 min read
Insertion in Binary Search Tree (BST) Given a BST, the task is to insert a new node in this BST.Example: How to Insert a value in a Binary Search Tree:A new key is always inserted at the leaf by maintaining the property of the binary search tree. We start searching for a key from the root until we hit a leaf node. Once a leaf node is fo
15 min read
Searching in Binary Search Tree (BST) Given a BST, the task is to search a node in this BST. For searching a value in BST, consider it as a sorted array. Now we can easily perform search operation in BST using Binary Search Algorithm. Input: Root of the below BST Output: TrueExplanation: 8 is present in the BST as right child of rootInp
7 min read
Deletion in Binary Search Tree (BST) Given a BST, the task is to delete a node in this BST, which can be broken down into 3 scenarios:Case 1. Delete a Leaf Node in BST Case 2. Delete a Node with Single Child in BSTDeleting a single child node is also simple in BST. Copy the child to the node and delete the node. Case 3. Delete a Node w
10 min read
Binary Search Tree (BST) Traversals – Inorder, Preorder, Post Order Given a Binary Search Tree, The task is to print the elements in inorder, preorder, and postorder traversal of the Binary Search Tree. Input: A Binary Search TreeOutput: Inorder Traversal: 10 20 30 100 150 200 300Preorder Traversal: 100 20 10 30 200 150 300Postorder Traversal: 10 30 20 150 300 200 1
10 min read
Balance a Binary Search Tree Given a BST (Binary Search Tree) that may be unbalanced, the task is to convert it into a balanced BST that has the minimum possible height.Examples: Input: Output: Explanation: The above unbalanced BST is converted to balanced with the minimum possible height.Input: Output: Explanation: The above u
10 min read
Self-Balancing Binary Search Trees Self-Balancing Binary Search Trees are height-balanced binary search trees that automatically keep the height as small as possible when insertion and deletion operations are performed on the tree. The height is typically maintained in order of logN so that all operations take O(logN) time on average
4 min read