Section (fiber bundle)

In the mathematical field of topology, a section (or cross section) of a fiber bundle is a continuous right inverse of the function . In other words, if is a fiber bundle over a base space,  :

then a section of that fiber bundle is a continuous map,

such that

A section is an abstract characterization of what it means to be a graph. The graph of a function can be identified with a function taking its values in the Cartesian product , of and :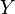

Let be the projection onto the first factor: . Then a graph is any function for which .

The language of fibre bundles allows this notion of a section to be generalized to the case when E is not necessarily a Cartesian product. If is a fibre bundle, then a section is a choice of point in each of the fibres. The condition simply means that the section at a point 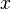must lie over 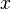. (See image.)

For example, when E is a vector bundle a section of E is an element of the vector space E_x lying over each point x ∈ B. In particular, a vector field on a smooth manifold M is a choice of tangent vector at each point of M: this is a section of the tangent bundle of M. Likewise, a 1-form on M is a section of the cotangent bundle.

Fiber bundle

In mathematics, and particularly topology, a fiber bundle (or, in British English, fibre bundle) is a space that is locally a product space, but globally may have a different topological structure. Specifically, the similarity between a space E and a product space B × F is defined using a continuous surjective map

that in small regions of E behaves just like a projection from corresponding regions of B × F to B. The map π, called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space E is known as the total space of the fiber bundle, B as the base space, and F the fiber.

In the trivial case, E is just B × F, and the map π is just the projection from the product space to the first factor. This is called a trivial bundle. Examples of non-trivial fiber bundles include the Möbius strip and Klein bottle, as well as nontrivial covering spaces. Fiber bundles such as the tangent bundle of a manifold and more general vector bundles play an important role in differential geometry and differential topology, as do principal bundles.

Bundle

Bundle or Bundling may refer to:

In marketing:

In economics:

In mathematics:

In medicine:

In computing:

Bundle (mathematics)

In mathematics, a bundle is a generalization of a fiber bundle dropping the condition of a local product structure. The requirement of a local product structure rests on the bundle having a topology. Without this requirement, more general objects can be considered bundles. For example, one can consider a bundle π: E→ B with E and B sets. It is no longer true that the preimages π ^{− 1}(x) must all look alike, unlike fiber bundles where the fibers must all be isomorphic (in the case of vector bundles) and homeomorphic.

Definition

A bundle is a triple (E, p, B) where E, B are sets and p:E→B a map.

This definition of a bundle is quite unrestrictive. For instance, the empty function defines a bundle. Nonetheless it serves well to introduce the basic terminology, and every type of bundle has the basic ingredients of above with restrictions on E, p, B and usually there is additional structure.

For each b ∈ B, p⁻¹(b) is the fibre or fiber of the bundle over b.

Section

Section may refer to:

Writing

Mathematics

Land area

Section (Alpine club)

The section (German: Sektion) of an Alpine club (or that of any such Alpine society or association) is an independent club or society that, together with the other sections, forms the main organisation ("Alpine club"). Membership of an Alpine club is normally only possible through membership of a section. The task of an Alpine club section is the maintenance of tradition and culture, the Alpine training of its members, the planning and implementation of mountain tours and expeditions, and also the maintenance of huts and trails in the mountains. Many sections own Alpine club huts. After the initial task of the Alpine clubs - i.e. the development of the Alps for tourism and Alpinism, was considered as largely completed in Central Europe today, the work of the sections moved increasingly into the service sector, including the organization of Alpine courses and tours as well as sponsoring climbing gyms.

Section (military unit)

A section is a military sub-subunit in some armies. In many armies, it might be a squad of 2-3 fireteams (i.e. seven to twelve soldiers). However, in France and armies based on the French model, it is the sub-division of a company (equivalent to a platoon).

Commonwealth

Australian Army

Under the new structure of the infantry platoon, sections are made up of eight men divided into two four-man fireteams. Each fireteam consists of a team leader (corporal/lance-corporal), a marksman with enhanced optics, a grenadier with an M203 and an LSW operator with an F89 Minimi light support weapon.

Typical fire team structure:

At the start of World War I, the Australian Army used a section that consisted of 27 men including the section commander, who was a non-commissioned officer holding the rank of sergeant.

During World War II, a rifle section comprised ten soldiers with a corporal in command with a lance-corporal as his second-in-command. The corporal used an M1928 Thompson submachine gun, while one of the privates used a Bren gun. The other eight soldiers all used No.1 Mk.3 Lee–Enfield rifles with a bayonet and scabbard. They all carried two or three No.36 Mills bomb grenades.