Rom er i matematikken en samlebetegnelse på flere typer objekter med en eller annen form for ekstra struktur. I dagligtale bruker man ofte begrepet til å betegne det tredimensjonale rommet vi lever i, men det finnes andre mer generelle eksempler slik som topologiske rom, vektorrom, grafer og mangfoldigheter.
Konseptet rom har ikke en presis matematisk definisjon, men brukes som en samlebetegnelse på mange ulike begreper. Dette fungerer på samme måte som for eksempel begrepet tall. Når man snakker om tall i matematikken må man spesifisere hvilken type tall man bruker — for eksempel naturlige tall, heltall, rasjonale tall eller reelle tall. Dette er fordi et tall i seg selv ikke har noen presis definisjon. På tilsvarende måte må man presisere hvilken type rom man bruker.
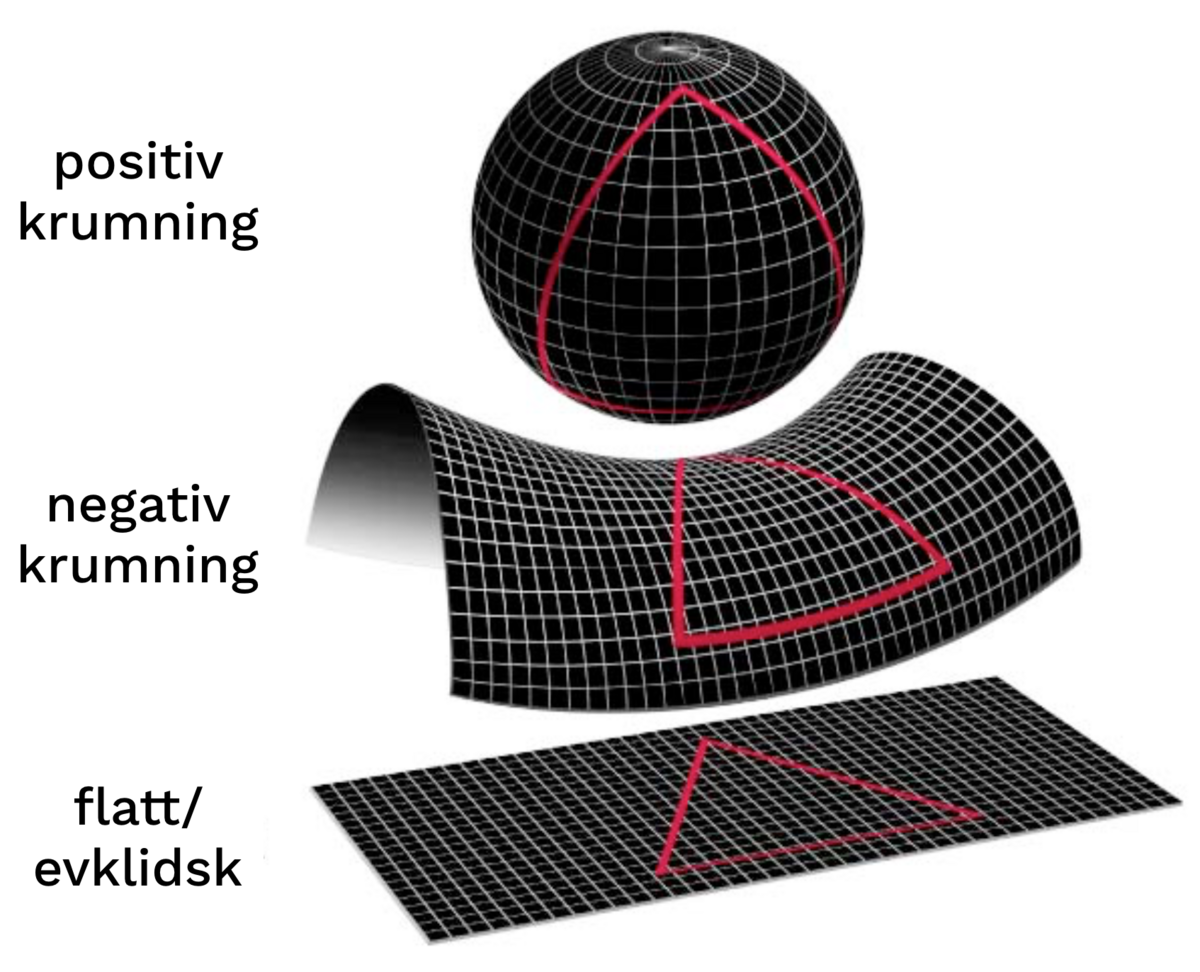
Selv om vi ikke har noen presis definisjon for hva et rom er, kan vi gi det en mer matematisk beskrivelse. Man kan for eksempel si at et rom er en mengde med en gitt struktur. Nicholas Bourbaki lagde en grov inndeling for ulike strukturer man kan ha, og delte dem inn i tre typer:
- topologiske strukturer
- algebraiske strukturer
- ordensstrukturer
Et rom kan også ha mer enn én struktur, og disse kan ofte flettes sammen på kompliserte måter.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.