File:Zeta0.5 100.svg

Original file (SVG file, nominally 680 × 800 pixels, file size: 93 KB)

Captions

English

Add a one-line explanation of what this file represents

Summary

DescriptionZeta0.5 100.svg	$\Re (\zeta ({\frac {1}{2}}+\mathrm {i} t))$ and $\Im (\zeta ({\frac {1}{2}}+\mathrm {i} t))$ English: Riemann-Zeta-function real and imaginary part on the critical line from 0 to 100. note that $\Re (\zeta (\textstyle {\frac {1}{2}}-\mathrm {i} t))=\Re (\zeta (\textstyle {\frac {1}{2}}+\mathrm {i} t))$ and $\Im (\zeta (\textstyle {\frac {1}{2}}-\mathrm {i} t))=-\Im (\zeta (\textstyle {\frac {1}{2}}+\mathrm {i} t))$
Date	December 2008
Source	Own work
Author	Geek3
Other versions	Zeta0.5 100 thin.svg, Zeta0.5 100 abs.svg

Mathematical Function Plot
Description	Plot of the Riemann Zeta function
Equation1 (blue)	$y=\Re (\zeta (\textstyle {\frac {1}{2}}+\mathrm {i} t))$
Equation2 (red)	$y=\Im (\zeta (\textstyle {\frac {1}{2}}+\mathrm {i} t))$
Coordinate System	Cartesian
X Range	0 .. 100
Y Range	$\mathbb {R}$
Accuracy	0.000001

W3C-validity not checked.

Licensing

I, the copyright holder of this work, hereby publish it under the following licenses:

Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.

This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic license.

You are free:

to share – to copy, distribute and transmit the work
to remix – to adapt the work

Under the following conditions:

attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

You may select the license of your choice.

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Dimensions	User	Comment
current	20:33, 7 September 2009	680 × 800 (93 KB)	Geek3 (talk \| contribs)	small error correction
	20:30, 7 September 2009	680 × 800 (93 KB)	Geek3 (talk \| contribs)	improved version
	17:44, 19 December 2008	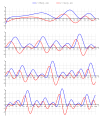680 × 800 (106 KB)	Geek3 (talk \| contribs)	{{Information \|Description=<math>\Re(\zeta(\frac{1}{2} + \mathrm{i}t))</math> and <math>\Im(\zeta(\frac{1}{2} + \mathrm{i}t))</math> {{en\|1=Riemann-Zeta-function real and imaginary part on the critical line from 0 to 100. note that <math>\Re(\

You cannot overwrite this file.

File usage on Commons

The following 2 pages use this file:

File usage on other wikis

The following other wikis use this file:

Usage on de.wikipedia.org
- Riemannsche Zeta-Funktion
Usage on en.wikipedia.org
- User:Promise her a definition
Usage on fr.wikipedia.org
- Fonction zêta de Riemann

Metadata

This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.

Short title

Zeta0.5_100.svg - real and imaginary Part of

    the Riemann-Zeta-function

on the critical line from 0 to 100

Image title

    Riemann-Zeta-function
    from Wikimedia Commons
    plot-range: real=1/2;  imaginary=[0 to 100]
    note that Re(Zeta(1/2 - ix)) =  Re(Zeta(1/2 + ix))
          and Im(Zeta(1/2 - ix)) = -Im(Zeta(1/2 + ix))

    plotted with several adapted cubic bezier-curves
    The plotcurve was calculated by some fancy code. The bezier-curve
    controlpoints are placed on tangents of the function-curve. They are
    furthermore positioned in a way to minimize the average quadratic distance
    between the bezier-curve and the function. This gives an accuracy, so that
    the deviation is in no point greater than 0.000001.

    symbols in "Computer Modern" (TeX) font embedded
    created with a plain text editor using GNU/Linux

    about: http://commons.wikimedia.org/wiki/Image:Zeta0.5_100.svg
    source: http://commons.wikimedia.org/
    rights: GNU Free Documentation license,
            Creative Commons Attribution ShareAlike license

Structured data

File:Zeta0.5 100.svg

Captions

Captions

Summary

Licensing

File history

File usage on Commons

File usage on other wikis

Metadata

Structured data

Items portrayed in this file

depicts

Riemann zeta function

creator

some value

copyright status

copyrighted

copyright license

Creative Commons Attribution-ShareAlike 2.0 Generic

GNU Free Documentation License, version 1.2 or later

Creative Commons Attribution-ShareAlike 1.0 Generic

Creative Commons Attribution-ShareAlike 2.5 Generic

Creative Commons Attribution-ShareAlike 3.0 Unported

source of file

original creation by uploader

inception

December 2008

Navigation menu

File:Zeta0.5 100.svg

Captions

Captions

Summary

Licensing

File history

File usage on Commons

File usage on other wikis

Metadata

Navigation menu

Search